题目内容
10.在△ABC中,a、b、c是三角形的三边,化简:$\sqrt{(a-b+c)^{2}}$-2$\sqrt{(c-a-b)^{2}}$.分析 先根据三角形的三边关系判断出a-b+c及c-a-b的符号,再把代数式进行化简即可.
解答 解:∵在△ABC中,a,b,c是三角形的三边长,
∴a-b+c>0,c-a-b<0,
∴原式=a-b+c-2[-(c-a-b)]
=a-b+c+2c-2a-2b
=-a-3b+3c.
点评 本题考查二次根式的性质与化简,三角形的三边关系,熟知三角形中,任意两边之和大于第三边是解答此题的关键.

练习册系列答案
相关题目
20.下列函数:①y=2x-1,②y=$\frac{1}{x}$,③y=-3x,④y=x2+1.其中是一次函数的有( )
| A. | ① | B. | ①③ | C. | ①②③ | D. | ①③④ |
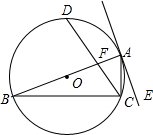 如图,AB是⊙O的直径,AE是⊙O的切线,C是⊙O上一点,CD平方∠ACB,若∠CAE=21°,则∠BFC的度数为114°.
如图,AB是⊙O的直径,AE是⊙O的切线,C是⊙O上一点,CD平方∠ACB,若∠CAE=21°,则∠BFC的度数为114°. 如图,线段AB的长为l.
如图,线段AB的长为l.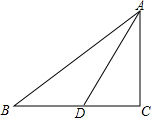 如图,在△ABC中,AD平分∠BAC,请利用线段之比可转化为面积之比的思路方法,求证:$\frac{BD}{DC}=\frac{AB}{AC}$.
如图,在△ABC中,AD平分∠BAC,请利用线段之比可转化为面积之比的思路方法,求证:$\frac{BD}{DC}=\frac{AB}{AC}$. 如图,在△ABC中,
如图,在△ABC中,