题目内容
13.先化简,再求值:($\frac{x+y}{x-y}$-$\frac{x-y}{x+y}$)•($\frac{1}{{x}^{2}}$-$\frac{1}{{y}^{2}}$),其中x=2+$\sqrt{3}$,y=2-$\sqrt{3}$.
分析 先根据分式混合运算的法则把原式进行化简,再把x、y的值代入进行计算即可.
解答 解:原式=$\frac{{x}^{2}+{y}^{2}+2xy-{x}^{2}-{y}^{2}+2xy}{(x-y)(x+y)}$•$\frac{-(x+y)(x-y)}{{x}^{2}{y}^{2}}$
=$\frac{4xy}{(x-y)(x+y)}$•$\frac{-(x+y)(x-y)}{{x}^{2}{y}^{2}}$
=-$\frac{4}{xy}$.
当x=2+$\sqrt{3}$,y=2-$\sqrt{3}$时,原式=-$\frac{4}{(2+\sqrt{3})(2-\sqrt{3})}$=-4.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
4.下列各运算中,正确的是( )
| A. | a2+a3=a5 | B. | (a+1)2=a2+1 | C. | $\sqrt{a}$•$\sqrt{b}$=$\sqrt{ab}$ | D. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ |
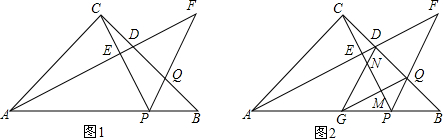
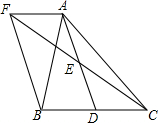 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.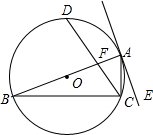 如图,AB是⊙O的直径,AE是⊙O的切线,C是⊙O上一点,CD平方∠ACB,若∠CAE=21°,则∠BFC的度数为114°.
如图,AB是⊙O的直径,AE是⊙O的切线,C是⊙O上一点,CD平方∠ACB,若∠CAE=21°,则∠BFC的度数为114°. 如图,线段AB的长为l.
如图,线段AB的长为l.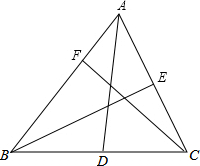 如图,在△ABC中,
如图,在△ABC中, 某五金厂生产的螺母形状如图所示,
某五金厂生产的螺母形状如图所示,