题目内容
17．解方程：①（3x-1）2-9（3x+1）2=0
②（2x-$\sqrt{3}$+$\sqrt{2}$）2=0．
分析 ①利用因式分解法解方程；
②利用直接开平方法解方程．
解答 解：①[3x-1+3（3x+1）][3x-1-3（3x+1）]=0，
3x-1+3（3x+1）=0或3x-1-3（3x+1）=0，
所以x1=-$\frac{1}{6}$，x2=$\frac{2}{3}$；
②2x-$\sqrt{3}$+$\sqrt{2}$=0
所以x1=x2=$\frac{\sqrt{3}-\sqrt{2}}{2}$．
点评 本题考查了解一元二次方程-因式分解法：先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．也考查了直接开平方法解一元二次方程．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
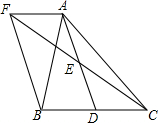如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF=BD，连接BF．
如图，线段AB的长为l．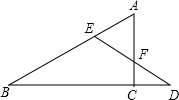
如图，在△ABC中，∠ACB=90°，D是BC延长线上一点，E是BD的垂直平分线与AB的交点，DE交AC于点F，求证：EA=EF．
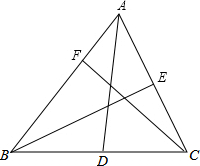如图，在△ABC中，