题目内容
9．过某个多边形一个顶点的所有对角线，把这个多边形分成5个三角形，这个多边形是（ ）| A． | 5 | B． | 6 | C． | 7 | D． | 8 |
分析 根据过某个多边形一个顶点画对角线，把多边形分成n-2个三角形，再结合题意可得n-2=5，再解即可．
解答 解：设多边形边数为n，
∵过某个多边形一个顶点的所有对角线，把这个多边形分成5个三角形，
∴n-2=5，
解得：n=7．
故选：C．
点评 此题主要考查了多边形的对角线，关键是掌握过某个多边形一个顶点画对角线，把多边形分成n-2个三角形．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
20．一个三角形三个内角的度数之比为1：2：3，则这个三角形一定是（ ）
| A． | 等腰三角形 | B． | 锐角三角形 | C． | 直角三角形 | D． | 钝角三角形 |
17．若ax=2，ay=3，则a3x-2y=（ ）
| A． | $\frac{8}{9}$ | B． | 72 | C． | 1 | D． | -1 |
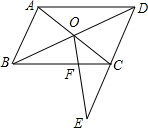如图，在?ABCD中，对角线AC与BD相交于点O，在DC的延长线上取一点E，连接OE交BC于点F．已知AB=4，BC=6，CE=2，则CF的长等于（ ）
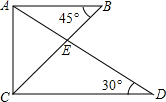一副三角尺拼成如图所示的图案，则∠CED的度数是105度．
1．下列各式计算正确的是（ ）
| A． | 8$\sqrt{2}$-3$\sqrt{2}$=5 | B． | 5$\sqrt{2}$+3$\sqrt{3}$=8$\sqrt{5}$ | C． | 4$\sqrt{2}$×3$\sqrt{3}$=12$\sqrt{6}$ | D． | 4$\sqrt{2}$÷2$\sqrt{2}$=2$\sqrt{2}$ |
如图是一个正方体的平面展开图，标注了数A的是正方体的正面，如果正方体的左面与右面标注式子相等．