题目内容

20．一个三角形三个内角的度数之比为1：2：3，则这个三角形一定是（　　）
A．等腰三角形B．锐角三角形C．直角三角形D．钝角三角形

分析 根据三角形内角和定理求出最大的内角的度数，再判断选项即可．

解答 解：∵三角形三个内角的度数之比为1：2：3，
∴此三角形的最大内角的度数是$\frac{3}{1+2+3}$×180°=90°，
∴此三角形为直角三角形，
故选C．

点评 本题考查了三角形内角和定理的应用，能求出三角形最大内角的度数是解此题的关键．

练习册系列答案
相关题目
10．比较大小：5＞$2\sqrt{6}$（填＜、＞或=）．
11．计算：
（1）（-8）+3+（-5）+8；
（2）（-5）×6+（-125）÷（-5）；
（3）（8$\frac{3}{4}$-$\frac{7}{8}$-$\frac{21}{20}$）÷（-$\frac{7}{8}$）；
（4）-32÷（-3）2-（-1）3×（$\frac{1}{3}$-$\frac{1}{2}$）．
8．25°12′8″=25.219度．
15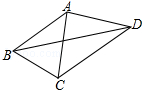．如图，已知AB=AC=AD，∠CBD=2∠BDC，∠BAC=42°，则∠CAD的度数为（　　）
A．110°B．88°C．84°D．66°
5．单项式2a2b的系数和次数分别是（　　）
A．2，2B．2，3C．3，2D．4，2
12．如果5x-3与-2x-9是互为相反数，求x的值．
9．过某个多边形一个顶点的所有对角线，把这个多边形分成5个三角形，这个多边形是（　　）
A．5B．6C．7D．8
10．先化简，再求值：（2x+1）（2x-1）-5x（x-1）+（x-1）2，其中x=-$\frac{1}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网