题目内容
4.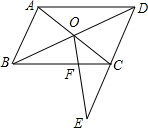 如图,在?ABCD中,对角线AC与BD相交于点O,在DC的延长线上取一点E,连接OE交BC于点F.已知AB=4,BC=6,CE=2,则CF的长等于( )
如图,在?ABCD中,对角线AC与BD相交于点O,在DC的延长线上取一点E,连接OE交BC于点F.已知AB=4,BC=6,CE=2,则CF的长等于( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 3 |
分析 过O作OM∥BC交CD于M,根据平行四边形的性质得到BO=DO,CD=AB=4,AD=BC=6,根据三角形的中位线的性质得到CM=$\frac{1}{2}$CD=2,OM=$\frac{1}{2}$BC=3,通过△CFE∽△EMO,根据相似三角形的性质得到$\frac{CF}{OM}=\frac{CE}{EM}$,代入数据即可得到结论.
解答 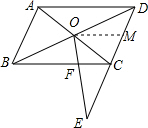 解:过O作OM∥BC交CD于M,
解:过O作OM∥BC交CD于M,
∵在?ABCD中,BO=DO,CD=AB=4,AD=BC=6,
∴CM=$\frac{1}{2}$CD=2,OM=$\frac{1}{2}$BC=3,
∵OM∥CF,
∴△CFE∽△EMO,
∴$\frac{CF}{OM}=\frac{CE}{EM}$,
即$\frac{CF}{3}=\frac{2}{4}$,
∴CF=1.5.
故选B.
点评 此题考查了平行四边形的性质、相似三角形的判定与性质等知识.解此题的关键是准确作出辅助线,合理应用数形结合思想解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.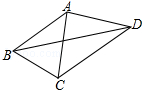 如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=42°,则∠CAD的度数为( )
如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=42°,则∠CAD的度数为( )
 如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=42°,则∠CAD的度数为( )
如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=42°,则∠CAD的度数为( )| A. | 110° | B. | 88° | C. | 84° | D. | 66° |
9.过某个多边形一个顶点的所有对角线,把这个多边形分成5个三角形,这个多边形是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
13.下列运算中错误的是( )
| A. | 3xy-(x2-2xy)=5xy-x2 | B. | 5x(2x2-y)=10x3-5xy | ||
| C. | 5mn(2m+3n-1)=10m2n+15mn2-1 | D. | [(a2b)2-1](a+b)=a5b2+a4b3-a-b |
 如图,在△ABC中,∠A=70°,点O到AB、BC、AC的距离相等,连接BO、CO,则∠BOC=125°.
如图,在△ABC中,∠A=70°,点O到AB、BC、AC的距离相等,连接BO、CO,则∠BOC=125°.