Question

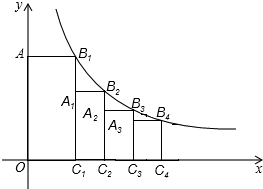如图，点B₁在反比例函数y=

2

x

（x＞0）的图象上，过点B₁分别作x轴和y轴的垂线，垂足为C₁和A，得到第一个矩形AOC₁B₁，点C₁的坐标为（1，0）；取x轴上一点C₂（

3

2

，0），过点C₂作x轴的垂线交反比例函数图象于点B₂，过B₂作线段B₂A₁⊥B₁C₁，交B₁C₁于点A₁，得到第二个矩形A₁C₁C₂B₂；依次在x轴上取点C₃（2，0），C₄（

5

2

，0）…按此规律作矩形，则第10个矩形A₉C₉C₁₀B₁₀的面积为

 

．

Answer 1

考点：反比例函数系数k的几何意义

专题：规律型

分析：根据反比例函数比例系数k的几何意义得到第1个矩形AOC₁B₁的面积=2，再利用反比例函数图象上点的坐标特征得到B₂点的坐标为（

3

2

，

4

3

），接着得到A₁的坐标为（1，

4

3

），则可根据反比例函数比例系数k的几何意义和两矩形的面积差得到第2个矩形A₁C₁C₂B₂的面积=

2

3

，同同样方法得到第3个矩形A₂C₂C₃B₃的面积=

2

4

，第4个矩形A₃C₃C₄B₄的面积=

2

5

，因此得到第n个矩形的面积为

2

n+1

，然后把n=10代入计算即可．

解答：解：第1个矩形AOC₁B₁的面积=2，
∵C₂（

3

2

，0），
∴B₂点的坐标为（

3

2

，

4

3

），
∴A₁的坐标为（1，

4

3

），
∴第2个矩形A₁C₁C₂B₂的面积=2-1×

4

3

=

2

3

；
∵C₃（2，0），
∴B₃点的坐标为（2，1），
∴A₂的坐标为（

3

2

，1），
∴第3个矩形A₂C₂C₃B₃的面积=2-1×

3

2

=

1

2

=

2

4

；
∵C₄（

5

2

，0），
∴B₄点的坐标为（

5

2

，

4

5

），
∴A₃的坐标为（2，

4

5

），
∴第4个矩形A₃C₃C₄B₄的面积=2-2×

4

5

=

2

5

，
…，
∴第10个矩形A₉C₉C₁₀B₁₀的面积=

2

10+1

=

2

11

．
故答案为

2

11

．

点评：本题考查了反比例函数比例系数k的几何意义：在反比例函数y=

k

x

图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．