题目内容
 如图,四边形ABCD是⊙O的内接四边形,如果∠AOC+∠ABC=90°,那么∠ADC的度数为
如图,四边形ABCD是⊙O的内接四边形,如果∠AOC+∠ABC=90°,那么∠ADC的度数为考点:圆内接四边形的性质,圆周角定理
专题:
分析:利用圆周角定理,得出∠B=x,则∠AOC=2x,利用圆内接四边形的性质得出∠ADC的度数.
解答:解:∵∠AOC+∠ABC=90°,∠B=
∠AOC,
∴设∠B=x,则∠AOC=2x,即x+2x=90,
解得:x=30,
故∠B+∠ADC=180°,
则∠ADC=150°.
故答案为:150°.
| 1 |
| 2 |
∴设∠B=x,则∠AOC=2x,即x+2x=90,
解得:x=30,
故∠B+∠ADC=180°,
则∠ADC=150°.
故答案为:150°.
点评:此题主要考查了圆周角定理以及圆内接四边形的性质,得出∠B的度数是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
a、b为有理数,a<0,b<0,且|a|>|b|,如果a,b,-a,-b在数轴上所对应的点分别为A、B、C、D,那么这四个点在数轴上从左到右的顺序依次为( )
| A、A B D C |
| B、C D B A |
| C、B A C D |
| D、B D C A |
若x2-x-m=(x-m)(x+1)且x≠0,则m等于( )
| A、-1 | B、0 | C、1 | D、2 |
若点(a,b)在第二象限,则点N(-a,-b-1)在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
若二次函数y=2x2的图象经过点P(1,a),则a的值为( )
A、
| ||
| B、1 | ||
| C、2 | ||
| D、4 |
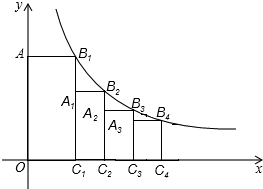 如图,点B1在反比例函数y=
如图,点B1在反比例函数y= 画出如图由11个小正方体搭成的几何体从不同角度看得到的图形.
画出如图由11个小正方体搭成的几何体从不同角度看得到的图形.