题目内容
 如图,⊙O是以原点为圆心,
如图,⊙O是以原点为圆心,| 2 |
| A、2 | ||
| B、4 | ||
C、3
| ||
D、
|
考点:切线的性质,一次函数图象上点的坐标特征
专题:计算题
分析:先根据坐标轴上点的坐标特征确定B(0,4),A(4,0),则可判断△OAB为等腰直角三角形,所以AB=
OA=4
,OH=
AB=2
,再根据切线的性质,由PQ为⊙O的切线得到OQ⊥PQ,根据勾股定理得到PQ=
=
,所以当OP最小时,PQ最小,根据垂线段最短得到OP=OH时,OP最小,即可计算出切线长PQ的最小值=
.
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| OP2-OQ2 |
| OP2-2 |
| 6 |
解答: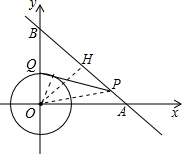 解:连结OP,OQ,作OH⊥AB于H,如图,
解:连结OP,OQ,作OH⊥AB于H,如图,
当x=0时,y=-x+4=4,则B(0,4);当y=0时,-x+4=0,解得x=4,则A(4,0),
∵OA=OB,
∴△OAB为等腰直角三角形,
∴AB=
OA=4
,
而OH⊥AB,
∴OH=
AB=2
,
∵PQ为⊙O的切线,
∴OQ⊥PQ,
在Rt△POQ中,PQ=
=
,
∴当OP最小时,PQ最小,
而OP=OH时,OP最小,
∴切线长PQ的最小值=
=
.
故选D.
 解:连结OP,OQ,作OH⊥AB于H,如图,
解:连结OP,OQ,作OH⊥AB于H,如图,当x=0时,y=-x+4=4,则B(0,4);当y=0时,-x+4=0,解得x=4,则A(4,0),
∵OA=OB,
∴△OAB为等腰直角三角形,
∴AB=
| 2 |
| 2 |
而OH⊥AB,
∴OH=
| 1 |
| 2 |
| 2 |
∵PQ为⊙O的切线,
∴OQ⊥PQ,
在Rt△POQ中,PQ=
| OP2-OQ2 |
| OP2-2 |
∴当OP最小时,PQ最小,
而OP=OH时,OP最小,
∴切线长PQ的最小值=
(2
|
| 6 |
故选D.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了一次函数图象上点的坐标特征.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
a、b为有理数,a<0,b<0,且|a|>|b|,如果a,b,-a,-b在数轴上所对应的点分别为A、B、C、D,那么这四个点在数轴上从左到右的顺序依次为( )
| A、A B D C |
| B、C D B A |
| C、B A C D |
| D、B D C A |
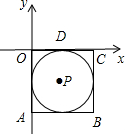 如图,在平面直角坐标xOy中,边长为2的正方形OABC的顶点A、C,分别在y轴负半轴和x轴正半轴上,顶点B在第四象限,圆P与正方形边都相切,与x轴切点为D,在⊙P上有一动点Q使得三角形ODQ为等腰三角形,请写出△OAC区域内所有符合条件的点Q的坐标
如图,在平面直角坐标xOy中,边长为2的正方形OABC的顶点A、C,分别在y轴负半轴和x轴正半轴上,顶点B在第四象限,圆P与正方形边都相切,与x轴切点为D,在⊙P上有一动点Q使得三角形ODQ为等腰三角形,请写出△OAC区域内所有符合条件的点Q的坐标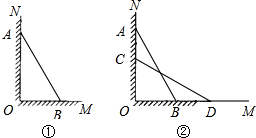 如图①,一个长为5m的梯子AB斜靠在与地面OM垂直的墙壁ON上,此时OB=
如图①,一个长为5m的梯子AB斜靠在与地面OM垂直的墙壁ON上,此时OB=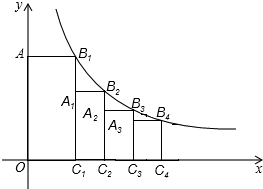 如图,点B1在反比例函数y=
如图,点B1在反比例函数y=