题目内容
5.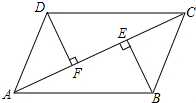 如图,AC是?ABCD的一条对角线,BE⊥AC,DF⊥AC,垂足分别为E,F.
如图,AC是?ABCD的一条对角线,BE⊥AC,DF⊥AC,垂足分别为E,F.(1)求证:△ADF≌△CBE;
(2)求证:四边形DFBE是平行四边形.
分析 (1)由平行四边形的性质得出AD∥BC,AD=BC,得出内错角相等∠DAF=∠BCE,证出∠AFD=∠CEB=90°,由AAS证明△ADF≌△CBE即可;
(2)由(1)得:△ADF≌△CBE,由全等三角形的性质得出DF=BE,再由BE∥DF,即可得出四边形DFBE是平行四边形.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠DAF=∠BCE,
∵BE⊥AC,DF⊥AC,
∴BE∥DF,∠AFD=∠CEB=90°,
在△ADF和△CBE中,$\left\{\begin{array}{l}{∠DAF=∠BCE}&{\;}\\{∠AFD=∠CEB}&{\;}\\{AD=CB}&{\;}\end{array}\right.$,
∴:△ADF≌△CBE(AAS);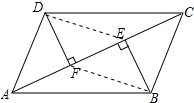
(2)解:如图所示:由(1)得:△ADF≌△CBE,
∴DF=BE,
∵BE∥DF,
∴四边形DFBE是平行四边形.
点评 本题考查了平行四边形的判定与性质、全等三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
20.直线$y=-\frac{{\sqrt{3}}}{3}x+2$与x轴,y轴分别交于A,B两点,把△AOB绕着A点旋转180°得到△AO′B′,则点B′的坐标为( )
| A. | (4,2) | B. | (4,-2) | C. | ($4\sqrt{3}$,2) | D. | ($4\sqrt{3}$,-2) |