题目内容
13.根据规律回答问题:12×18=1×(1+1)×100+2×8=216
23×27=2×(2+1)×100+3×7=621
84×86=8×(8+1)×100+4×6=7224
(1)根据规律计算:952=9025.
(2)用含有n和m的式子表示上面的规律并证明.
分析 审题发现每个算式的个位数字之和等于10,十位数字相同,而结果等于各位数字与比它大1的数的积的100倍,再加上个位数字的积,根据所得规律进行计算即可.
解答 解:
(1)由已知总结出规律“若每个算式的个位数字之和等于10,十位数字相同,则结果等于各位数字与比它大1的数的积的100倍,再加上个位数字的积”
所以952=9×(9+1)×100+5×5=9025
故答案为9025.
(2)若一个两位数的个位数字是m,十位数字为n,表示为:10n+m;则另一个数的个位数字为10-m,十位数字是n,表示为:10n+(10-m),
(10n+m)×[10n+(10-m)]=n(n+1)×100+m(10-m),
证明:若一个两位数的个位数字是m,十位数字为n,表示为:10n+m;则另一个数的个位数字为10-m,十位数字是n,表示为:10n+(10-m)=10n-m+10
所以:(10n+m)×(10n-m+10)=100n2+100n+10m-m2=n(n+1)×100+m(10-m)
点评 此题主要考察规律探索以及整式的运算和分解,综合性较强,在已有的运算中合理分析,发现规律是解决第一个问题的关键,在第二问中要熟悉数字的表示方法,并结合整式的运算和分解进行,认真的学习态度很重要.

练习册系列答案
相关题目
3. 如图,在△ABC中,AB=AC,∠A=140°,延长BC至点D,则∠ACD等于( )
如图,在△ABC中,AB=AC,∠A=140°,延长BC至点D,则∠ACD等于( )
 如图,在△ABC中,AB=AC,∠A=140°,延长BC至点D,则∠ACD等于( )
如图,在△ABC中,AB=AC,∠A=140°,延长BC至点D,则∠ACD等于( )| A. | 130° | B. | 140° | C. | 150° | D. | 160° |
4.利用因式分解计算22014-22013,则结果是( )
| A. | 22013 | B. | 1 | C. | 2 | D. | 22012 |
1.下列命题正确的是( )
| A. | 一组对边平行,一组对边相等的四边形是平行四边形 | |
| B. | 对角线互相垂直的平行四边形是菱形 | |
| C. | 如果顺次连结一个四边形各边中点得到的是一个正方形,那么原四边形一定是正方形 | |
| D. | 对角线相等的四边形是矩形 |
8.某生产小组有15名工人,调查每个工人的日均零件生产能力,获得如表数据:
(1)求这15名工人日均生产零件的众数、中位数、平均数.
(2)为提高工作效率和工人的工作积极性,生产管理者准备实行“每天定额生产,超产有奖”的措施,如果你是管理者,你将如何确定这个定额?请说明理由.
| 日均生产零件的个数(个) | 5 | 6 | 7 | 8 | 9 | 10 |
| 工人人数(人) | 3 | 2 | 2 | 3 | 4 | 1 |
(2)为提高工作效率和工人的工作积极性,生产管理者准备实行“每天定额生产,超产有奖”的措施,如果你是管理者,你将如何确定这个定额?请说明理由.
18.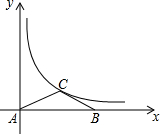 如图,等腰三角形ABC的顶点A在原点,顶点B在x轴的正半轴上,顶点C在函数y=$\frac{k}{x}$(x>0)的图象上运动,且AC=BC,则△ABC的面积大小变化情况是( )
如图,等腰三角形ABC的顶点A在原点,顶点B在x轴的正半轴上,顶点C在函数y=$\frac{k}{x}$(x>0)的图象上运动,且AC=BC,则△ABC的面积大小变化情况是( )
 如图,等腰三角形ABC的顶点A在原点,顶点B在x轴的正半轴上,顶点C在函数y=$\frac{k}{x}$(x>0)的图象上运动,且AC=BC,则△ABC的面积大小变化情况是( )
如图,等腰三角形ABC的顶点A在原点,顶点B在x轴的正半轴上,顶点C在函数y=$\frac{k}{x}$(x>0)的图象上运动,且AC=BC,则△ABC的面积大小变化情况是( )| A. | 一直不变 | B. | 先增大后减小 | C. | 先减小后增大 | D. | 先增大后不变 |
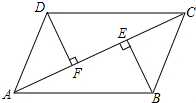 如图,AC是?ABCD的一条对角线,BE⊥AC,DF⊥AC,垂足分别为E,F.
如图,AC是?ABCD的一条对角线,BE⊥AC,DF⊥AC,垂足分别为E,F.