题目内容
10.若关于x的方程$\frac{3x+1}{2}$-2=$\frac{3x-2}{10}$-$\frac{2a+3}{5}$的解与关于x的方程3x+$\frac{a-1}{2}$=3的解相同,求a的值.分析 分别解出两方程的解,两解相等,就得到关于a的方程,从而可以求出a的值.
解答 解:由$\frac{3x+1}{2}$-2=$\frac{3x-2}{10}$-$\frac{2a+3}{5}$解得
x=$\frac{-4a+9}{12}$
由3x+$\frac{a-1}{2}$=3解得
x=$\frac{7-a}{6}$.
关于x的方程$\frac{3x+1}{2}$-2=$\frac{3x-2}{10}$-$\frac{2a+3}{5}$的解与关于x的方程3x+$\frac{a-1}{2}$=3的解相同,得
$\frac{-4a+9}{12}$=$\frac{7-a}{6}$.
解得a=-$\frac{5}{2}$,
a的值为-$\frac{5}{2}$.
点评 本题考查了同解方程,利用同解方程的出关于a的方程是解题关键.

练习册系列答案
相关题目
1.下列命题正确的是( )
| A. | 一组对边平行,一组对边相等的四边形是平行四边形 | |
| B. | 对角线互相垂直的平行四边形是菱形 | |
| C. | 如果顺次连结一个四边形各边中点得到的是一个正方形,那么原四边形一定是正方形 | |
| D. | 对角线相等的四边形是矩形 |
18.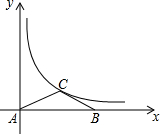 如图,等腰三角形ABC的顶点A在原点,顶点B在x轴的正半轴上,顶点C在函数y=$\frac{k}{x}$(x>0)的图象上运动,且AC=BC,则△ABC的面积大小变化情况是( )
如图,等腰三角形ABC的顶点A在原点,顶点B在x轴的正半轴上,顶点C在函数y=$\frac{k}{x}$(x>0)的图象上运动,且AC=BC,则△ABC的面积大小变化情况是( )
 如图,等腰三角形ABC的顶点A在原点,顶点B在x轴的正半轴上,顶点C在函数y=$\frac{k}{x}$(x>0)的图象上运动,且AC=BC,则△ABC的面积大小变化情况是( )
如图,等腰三角形ABC的顶点A在原点,顶点B在x轴的正半轴上,顶点C在函数y=$\frac{k}{x}$(x>0)的图象上运动,且AC=BC,则△ABC的面积大小变化情况是( )| A. | 一直不变 | B. | 先增大后减小 | C. | 先减小后增大 | D. | 先增大后不变 |
15.估算$\sqrt{29}$-2的值( )
| A. | 在1至2之间 | B. | 在2至3之间 | C. | 在3至4之间 | D. | 在4至5之间 |
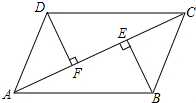 如图,AC是?ABCD的一条对角线,BE⊥AC,DF⊥AC,垂足分别为E,F.
如图,AC是?ABCD的一条对角线,BE⊥AC,DF⊥AC,垂足分别为E,F.