题目内容
16.请完成下面的说明: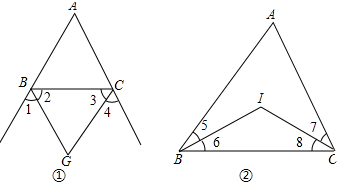
(1)如图(1)所示,△ABC的外角平分线交于点G,试说明∠BGC=90°-$\frac{1}{2}$∠A.
(2)如图(2)所示,若△ABC的内角平分线交于点I,试说明∠BIC=90°+$\frac{1}{2}$∠A.
(3)根据(1),(2)的结论,你能说出∠BGC和∠BIC的关系吗?
分析 (1)根据三角形外角性质和三角形内角和定理得出∠EBC=∠A+∠ACB,∠FCB=∠A+∠ACB,∠A+∠ABC+∠CBA=180°,求出∠EBC+∠FCB=180°+∠A,求出∠2+∠3的度数,即可得出答案;
(2)求出∠6+∠8的度数,根据三角形内角和定理求出即可;
(3)根据(1)(2)的结论即可得出答案.
解答 解(1)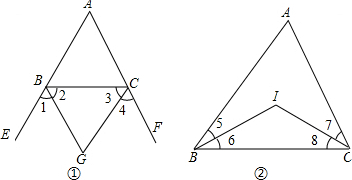
如图1,∵∠EBC=∠A+∠ACB,∠FCB=∠A+∠ACB,∠A+∠ABC+∠CBA=180°,
∴∠EBC+∠FCB=180°+∠A,
∵BG、CG分别平分∠EBC、∠FCB,
∴$∠2+∠3=\frac{1}{2}({∠EBC+∠FCB})=\frac{1}{2}({180°+∠A})=90°+\frac{1}{2}∠A$,
∴$∠BGC=180°-({∠2+∠3})=90°-\frac{1}{2}∠A$;
(2)∵BI、CI分别平分∠ABC、∠ACB,
∴$∠6+∠8=\frac{1}{2}({∠ABC+∠ACB})=\frac{1}{2}({180°-∠A})=90°-\frac{1}{2}∠A$,
∴$∠BIC=180°-({∠6+∠8})=90°+\frac{1}{2}∠A$,
即$∠BIC=90°+\frac{1}{2}∠A$;
(3)∠BGC和∠BIC的关系是互补.
点评 本题考查了三角形内角和定理,三角形外角性质的应用,能正确根据定理进行推理是解此题的关键.

练习册系列答案
相关题目
4.利用因式分解计算22014-22013,则结果是( )
| A. | 22013 | B. | 1 | C. | 2 | D. | 22012 |
1.下列命题正确的是( )
| A. | 一组对边平行,一组对边相等的四边形是平行四边形 | |
| B. | 对角线互相垂直的平行四边形是菱形 | |
| C. | 如果顺次连结一个四边形各边中点得到的是一个正方形,那么原四边形一定是正方形 | |
| D. | 对角线相等的四边形是矩形 |
8.某生产小组有15名工人,调查每个工人的日均零件生产能力,获得如表数据:
(1)求这15名工人日均生产零件的众数、中位数、平均数.
(2)为提高工作效率和工人的工作积极性,生产管理者准备实行“每天定额生产,超产有奖”的措施,如果你是管理者,你将如何确定这个定额?请说明理由.
| 日均生产零件的个数(个) | 5 | 6 | 7 | 8 | 9 | 10 |
| 工人人数(人) | 3 | 2 | 2 | 3 | 4 | 1 |
(2)为提高工作效率和工人的工作积极性,生产管理者准备实行“每天定额生产,超产有奖”的措施,如果你是管理者,你将如何确定这个定额?请说明理由.
 如图所示,已知∠1+∠2=180°,∠3=∠B.试判断直线DE和直线BC的位置关系.并说明理由.
如图所示,已知∠1+∠2=180°,∠3=∠B.试判断直线DE和直线BC的位置关系.并说明理由.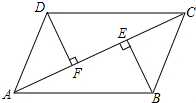 如图,AC是?ABCD的一条对角线,BE⊥AC,DF⊥AC,垂足分别为E,F.
如图,AC是?ABCD的一条对角线,BE⊥AC,DF⊥AC,垂足分别为E,F.