题目内容
20.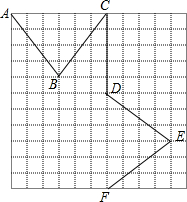 一只小虫从A点出发,沿着图中折线到F点取食,请你计算一下,它一共走了多少路程.(写出过程)
一只小虫从A点出发,沿着图中折线到F点取食,请你计算一下,它一共走了多少路程.(写出过程)
分析 由勾股定理得出AB=BC=DE=EF=$\sqrt{{3}^{2}+{4}^{2}}$=5,即可得出答案.
解答 解:由勾股定理得:AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,BC=$\sqrt{{3}^{2}+{4}^{2}}$=5,DE=$\sqrt{{3}^{2}+{4}^{2}}$=5,EF=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴AB+BC+CD+DE+EF=5×4+5=25,
答:它一共走了25个单位长度的路程.
点评 本题考查勾股定理的应用,关键是找到直角三角形的直角边,根据勾股定理得解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列运算正确的是( )
| A. | (a-b)2=a2-b2 | B. | (2a+1)(2a-1)=4a-1 | C. | (-2a3)2=4a6 | D. | x2-8x+16=(x+4)2 |

 如图,一只蚂蚁从长、宽都是2,高是5的长方体纸盒的A点沿纸盒面爬到B点,那么它所行的最短路线的长是$\sqrt{41}$.
如图,一只蚂蚁从长、宽都是2,高是5的长方体纸盒的A点沿纸盒面爬到B点,那么它所行的最短路线的长是$\sqrt{41}$.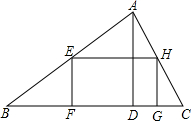 如图,在△ABC中,AD是BC上的高,且BC=9,AD=3,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,如果设边EF的长为x(0<x<3),矩形EFGH的面积为y,那么y关于x的函数解析式是y=-3x2+9x(0<x<3).
如图,在△ABC中,AD是BC上的高,且BC=9,AD=3,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,如果设边EF的长为x(0<x<3),矩形EFGH的面积为y,那么y关于x的函数解析式是y=-3x2+9x(0<x<3).