题目内容
15.用正方形硬纸板做三棱柱盒子,每个盒子由3个长方形侧面和2个等边三角形底面组成,硬纸板用如图两种方法裁剪(裁剪后边角料不再利用).
现有19张硬纸板,其中x张硬纸板用方法一裁剪,其余硬纸板用方法二裁剪.
(1)分别求裁剪出的侧面和底面的个数.(用含x的代数式表示)
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
分析 (1)由x张用方法一,就有(19-x)张用方法二,就可以分别表示出侧面个数和底面个数;
(2)根据裁剪出的侧面和底面恰好全部用完得出方程,解方程求出x的值,求出侧面的总数就可以求出结论.
解答 解:(1)侧面个数:6x+4(19-x)=(2x+76)个.
底面个数:5(19-x)=(95-5x)个.
(2)由题意,得$\frac{2x+76}{3}=\frac{95-5x}{2}$.
解得:x=7.
$\frac{2x+76}{3}=\frac{2×7+76}{3}=30$(个).
答:若裁剪出的侧面和底面恰好全部用完,能做30个盒子.
点评 本题考查了列一元一次方程解实际问题的运用,一元一次方程的解法的运用,列代数式的运用,解答时根据裁剪出的侧面和底面个数相等建立方程是关键.

练习册系列答案
相关题目
3.赵先生手中有一张记录他从出生到24周岁期间的身高情况表(如下):
下列说法中错误的是( )
| 年龄x/岁 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| 身高h/cm | 48 | 100 | 130 | 140 | 150 | 158 | 165 | 170 | 170.4 |
| A. | 赵先生的身高增长速度总体上先快后慢 | |
| B. | 赵先生的身高在21岁以后基本不长了 | |
| C. | 赵先生的身高从0岁到12岁平均每年增高12.5cm | |
| D. | 赵先生的身高从0岁到24岁平均每年增高5.1cm |
 如图,有两条公路OM,ON相交成30°角.沿公路OM方向离O点80米处有一所学校A,当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若已知重型运输卡车P沿道路ON方向行驶的速度为18千米/时.
如图,有两条公路OM,ON相交成30°角.沿公路OM方向离O点80米处有一所学校A,当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若已知重型运输卡车P沿道路ON方向行驶的速度为18千米/时.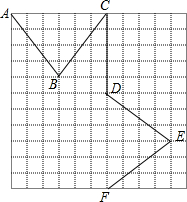 一只小虫从A点出发,沿着图中折线到F点取食,请你计算一下,它一共走了多少路程.(写出过程)
一只小虫从A点出发,沿着图中折线到F点取食,请你计算一下,它一共走了多少路程.(写出过程)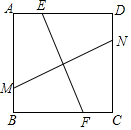 如图,正方形ABCD内有两条相交线段MN、EF,M、N、E、F分别在边AB、CD、AD、BC上.
如图,正方形ABCD内有两条相交线段MN、EF,M、N、E、F分别在边AB、CD、AD、BC上.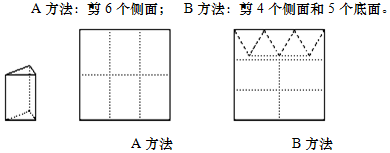
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①a>0;②b>0;③c<0;b2-4ac>0中,正确的个数有( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①a>0;②b>0;③c<0;b2-4ac>0中,正确的个数有( )