题目内容
6.已知a、b为实数,关于x的不等式组$\left\{\begin{array}{l}15x-b≤0\\ 20x+a>0\end{array}\right.$的整数解仅2、3、4.则ab的最大值是-1200.分析 首先解不等式组,用a,b表示出不等式组的解集,根据不等式的整数解仅有3,4,5,即可确定a,b的值,从而求解.
解答 解:解不等式组不等式组$\left\{\begin{array}{l}15x-b≤0\\ 20x+a>0\end{array}\right.$得:-$\frac{a}{20}$<x≤$\frac{b}{15}$,
∵整数解仅有2,3,4,
∴1≤-$\frac{a}{20}$<2,4≤$\frac{b}{15}$<5,
解得:-40<a≤-20,60≤b<75,
∴ab的最大值为-1200.
故答案为-1200.
点评 本题考查了不等式的整数解及解不等式组的能力,根据整数解确定ab的最大值是关键.

练习册系列答案
相关题目
11.下列各数中,能与$\sqrt{3}$合并的是( )
| A. | $\sqrt{24}$ | B. | $\sqrt{32}$ | C. | $\sqrt{96}$ | D. | $\sqrt{\frac{3}{4}}$ |
18.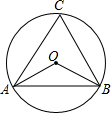 如图,△ABC是⊙O的内接三角形,若∠C=60°,则∠AOB的度数是( )
如图,△ABC是⊙O的内接三角形,若∠C=60°,则∠AOB的度数是( )
 如图,△ABC是⊙O的内接三角形,若∠C=60°,则∠AOB的度数是( )
如图,△ABC是⊙O的内接三角形,若∠C=60°,则∠AOB的度数是( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |