题目内容
16.计算:(1)2$\sqrt{3}$-$\sqrt{8}$$+\frac{1}{2}\sqrt{12}+\frac{1}{5}\sqrt{50}$
(2)$\frac{x}{2x-3}+\frac{5}{3-2x}$=4.
分析 (1)先化简,然后在合并同类二次根式即可;
(2)先确定最简公分母为2x-3,然后在去分母,将分式方程转化为整式方程,接下来,求得整式方程的解,最后检验即可.
解答 解:(1)2$\sqrt{3}$-2$\sqrt{2}$+$\sqrt{3}$+$\sqrt{2}$=3$\sqrt{3}$-$\sqrt{2}$;
(2)原方程可变形为$\frac{x}{2x-3}-\frac{5}{2x-3}$=4.
去分母得:x-5=4(2x-3),
解得:x=1,
当x=1时,2x-3≠0,
所以x=1是原方程的解.
点评 本题主要考查的是二次根式的加减、解分式方程,将各二次根式化简为最简二次根式是解(1)的关键,将分式方程转为整式方程是解(2)的关键.

练习册系列答案
相关题目
11.若(x+4)(x-2)=x2+mx+m,则m、n的值分别是( )
| A. | 2,8 | B. | -2,-8 | C. | -2,8 | D. | 2,-8 |
1.图1是一个边长为1的等边三角形和一个菱形的组合图形,菱形边长为等边三角形边长的一半,以此为基本单位,可以拼成一个形状相同但尺寸更大的图形(如图2),依此规律继续拼下去(如图3)…,则第6个图形的周长是( )
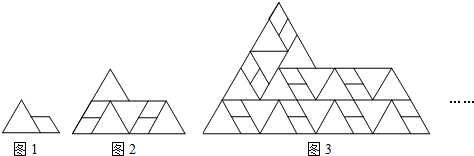

| A. | 32 | B. | 64 | C. | 128 | D. | 256 |
6.某班科技兴趣小组的学生,将自己的作品向本组其他成员各赠送一件,全组共相互赠送作品56件,若全组有x名同学,则根据题意列出的方程是( )
| A. | x(x-1)=56×2 | B. | 2x(x+1)=56 | C. | x(x+1)=56 | D. | x(x-1)=56 |