题目内容
11．设a，b，c是不全相等的任意实数，若x=b2-ac，y=c2-ab，z=a2-bc．求证：x，y，z至少有一个大于零．分析 假设x，y，z都小于零，列出算式，根据完全平方公式把原式变形，根据偶次方的非负性判断即可．
解答 解：假设x，y，z都小于零，
则b2-ac+c2-ab+a2-bc＜0，
2b2-2ac+2c2-2ab+2a2-2bc＜0，
（a-b）2+（a-c）2+（b-c）2＜0，
这与偶次方的非负性相矛盾，
∴假设不成立，
∴x，y，z至少有一个大于零．
点评 本题考查的是反证法的应用，反证法的一般步骤是：①假设命题的结论不成立；②从这个假设出发，经过推理论证，得出矛盾；③由矛盾判定假设不正确，从而肯定原命题的结论正确．
练习册系列答案
口算题天天练系列答案
相关题目
1．
如图，A，O，B在一条直线上，∠1=∠2，∠3=∠4，则图中互余的角共有（ ）
如图，A，O，B在一条直线上，∠1=∠2，∠3=∠4，则图中互余的角共有（ ）| A． | 5对 | B． | 4对 | C． | 3对 | D． | 2对 |
2．在下列实数中，无理数是（ ）
| A． | 3.1415926 | B． | $\frac{22}{7}$ | C． | $\sqrt{3}$ | D． | $\sqrt{\frac{4}{9}}$ |
19．下列说法中正确的是（ ）
| A． | x的系数是0 | B． | y的次数是0 | ||
| C． | 23xy是二次单项式 | D． | 32与42不是同类项 |
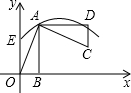如图，抛物线y=ax2+$\frac{7}{5}$x+c经过点A（2，4），E（0，2），AB⊥x轴于点B．