题目内容
如图①,直角三角形AOB中,∠AOB=90°,AB平行于x轴,OA=2OB,AB=5,反比例函数y=
(x>0)的图象经过点A.
(1)直接写出反比例函数的解析式;
(2)如图②,P(x,y)在(1)中的反比例函数图象上,其中1<x<8,连接OP,过点O 作OQ⊥OP,且OP=2OQ,连接PQ.设点Q坐标为(m,n),其中m<0,n>0,求n与m的函数解析式,并直接写出自变量m的取值范围;
(3)在(2)的条件下,若Q坐标为(m,1),求△POQ的面积.

| k |
| x |
(1)直接写出反比例函数的解析式;
(2)如图②,P(x,y)在(1)中的反比例函数图象上,其中1<x<8,连接OP,过点O 作OQ⊥OP,且OP=2OQ,连接PQ.设点Q坐标为(m,n),其中m<0,n>0,求n与m的函数解析式,并直接写出自变量m的取值范围;
(3)在(2)的条件下,若Q坐标为(m,1),求△POQ的面积.

考点:反比例函数综合题
专题:综合题
分析:(1)如图①,在Rt△OAB中利用勾股定理计算出OB=
,OA=2
,由于AB平行于x轴,则OC⊥AB,则可利用面积法计算出OC=2,在Rt△AOC中,根据勾股定理可计算出AC=4,得到A点坐标为(4,2),然后利用待定系数法确定反比例函数解析式为y=
;
(2)分别过P、Q做x轴垂线,垂足分别为H、D,如图②,先证明Rt△POH∽Rt△OQD,根据相似的性质得
=
=
,由于OP=2OQ,PH=y,OH=x,OD=-m,QD=n,则
=
=2,即有x=2n,y=-2m,而x、y满足y=
,则2n•(-2m)=8,即mn=-2,当1<x<8时,1<y<8,所以1<-2m<8,解得-4<m<-
;
(3)由于n=1时,m=-2,即Q点坐标为(-2,1),利用两点的距离公式计算出OQ=
,则OP=2OQ=2
,然后根据三角形面积公式求解.
| 5 |
| 5 |
| 8 |
| x |
(2)分别过P、Q做x轴垂线,垂足分别为H、D,如图②,先证明Rt△POH∽Rt△OQD,根据相似的性质得
| OH |
| QD |
| PH |
| OD |
| OP |
| OQ |
| x |
| n |
| y |
| -m |
| 8 |
| x |
| 1 |
| 2 |
(3)由于n=1时,m=-2,即Q点坐标为(-2,1),利用两点的距离公式计算出OQ=
| 5 |
| 5 |
解答:解:(1)如图①,∵∠AOB=90°,
∴OA2+OB2=AB2,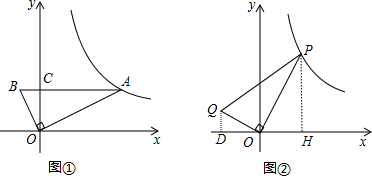
∵OA=2OB,AB=5,
∴4OB2+OB2=25,解得OB=
,
∴OA=2
,
∵AB平行于x轴,
∴OC⊥AB,
∴
OC•AB=
OB•OA,即OC=
=2,
在Rt△AOC中,AC=
=4,
∴A点坐标为(4,2),
设过A点的反比例函数解析式为y=
,
∴k=4×2=8,
∴反比例函数解析式为y=
;
(2)分别过P、Q作x轴垂线,垂足分别为H、D,如图②,
∵OQ⊥OP,
∴∠POH+∠QOD=90°,
∵∠POH+∠OPH=90°,
∴∠QOD=∠OPH,
∴Rt△POH∽Rt△OQD,
∴
=
=
,
∵P(x,y)在(1)中的反比例函数图象上,其中1<x<8,Q点坐标为(m,n),其中m<0,n>0,OP=2OQ,
∴PH=y,OH=x,OD=-m,QD=n,
∴
=
=2,解得x=2n,y=-2m,
∵y=
,
∴2n•(-2m)=8,
∴mn=-2(-4<m<-
);
(3)∵n=1时,m=-2,即Q点坐标为(-2,1),
∴OQ=
=
,
∴OP=2OQ=2
,
∴S△POQ=
×
×2
=5.
∴OA2+OB2=AB2,

∵OA=2OB,AB=5,
∴4OB2+OB2=25,解得OB=
| 5 |
∴OA=2
| 5 |
∵AB平行于x轴,
∴OC⊥AB,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| ||||
| 5 |
在Rt△AOC中,AC=
| OA2-OC2 |
∴A点坐标为(4,2),
设过A点的反比例函数解析式为y=
| k |
| x |
∴k=4×2=8,
∴反比例函数解析式为y=
| 8 |
| x |
(2)分别过P、Q作x轴垂线,垂足分别为H、D,如图②,
∵OQ⊥OP,
∴∠POH+∠QOD=90°,
∵∠POH+∠OPH=90°,
∴∠QOD=∠OPH,
∴Rt△POH∽Rt△OQD,
∴
| OH |
| QD |
| PH |
| OD |
| OP |
| OQ |
∵P(x,y)在(1)中的反比例函数图象上,其中1<x<8,Q点坐标为(m,n),其中m<0,n>0,OP=2OQ,
∴PH=y,OH=x,OD=-m,QD=n,
∴
| x |
| n |
| y |
| -m |
∵y=
| 8 |
| x |
∴2n•(-2m)=8,
∴mn=-2(-4<m<-
| 1 |
| 2 |
(3)∵n=1时,m=-2,即Q点坐标为(-2,1),
∴OQ=
| 12+(-2)2 |
| 5 |
∴OP=2OQ=2
| 5 |
∴S△POQ=
| 1 |
| 2 |
| 5 |
| 5 |
点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征和待定系数法求反比例函数解析式;理解坐标与图形的性质;会利用相似比和勾股定理进行几何计算.

练习册系列答案
相关题目
 如图,平面直角坐标系中,△ABC的顶点都在网格点上.
如图,平面直角坐标系中,△ABC的顶点都在网格点上. 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且BD=DC,连接BF,求证:四边形AFBD为平行四边形.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且BD=DC,连接BF,求证:四边形AFBD为平行四边形. 如图,已知半径为2的⊙O与直线x相切于点A,点P 是直径AB左侧半圆上的动点,过点P作直线x的垂线,垂足为C,PC与⊙O交于点D,连接PA、PB,设PC的长为x(2<x<4).
如图,已知半径为2的⊙O与直线x相切于点A,点P 是直径AB左侧半圆上的动点,过点P作直线x的垂线,垂足为C,PC与⊙O交于点D,连接PA、PB,设PC的长为x(2<x<4). 如图,△ABC的边AB为⊙O的直径,BC与圆交于点D,D为BC的中点,过D作DE⊥AC于E.
如图,△ABC的边AB为⊙O的直径,BC与圆交于点D,D为BC的中点,过D作DE⊥AC于E. 如图,平行四边形ABCD中,AC平分∠BAD.求证:四边形ABCD是菱形.
如图,平行四边形ABCD中,AC平分∠BAD.求证:四边形ABCD是菱形.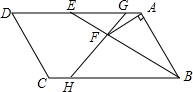 如图,?ABCD中,E为AD边上一点,AE=AB,AF⊥AB,交线段BE于点F,G为AE上一点,AG:GE=1:5,连结GF并延长交边BC于点H.若GE:BH=1:2,则tan∠GHB=
如图,?ABCD中,E为AD边上一点,AE=AB,AF⊥AB,交线段BE于点F,G为AE上一点,AG:GE=1:5,连结GF并延长交边BC于点H.若GE:BH=1:2,则tan∠GHB= 如图,点D、E、F分别是△ABC各边中点,若AB=AC=10,BC=12,则四边形ADEF的周长为
如图,点D、E、F分别是△ABC各边中点,若AB=AC=10,BC=12,则四边形ADEF的周长为