题目内容
8.函数y=$\frac{x+1}{{\sqrt{x-3}}}$的自变量x的取值范围是x>3.分析 根据二次根式的性质和分式的意义,被开方数大于或等于0,分母不等于0,可以求出x的范围.
解答 解:根据题意得:x-3≥0且x-3≠0,
解得:x>3.
故答案为x>3.
点评 本题考查了函数自变量的取值范围问题,函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
18.某服装厂准备加工400套运动装,在加工完160套后,采用了新技术,使得工作效率比原计划提高了20%,结果共用了18天完成任务,问计划每天加工服装多少套?在这个问题中,设计划每天加工x套服装,则根据题意可得方程为( )
| A. | $\frac{160}{x}$+$\frac{400-160}{(1+20%)x}$=18 | B. | $\frac{160}{x}$+$\frac{400}{(1+20%)x}$=18 | ||
| C. | $\frac{160}{x}$+$\frac{400-160}{20%x}$=18 | D. | $\frac{400}{x}$+$\frac{400-160}{(1+20%)x}$=18 |
19.若$\frac{{\sqrt{x-3}}}{x-1}$在实数范围内有意义,则x的取值范围是( )
| A. | x≥3 | B. | x≤3且x≠1 | C. | 1<x≤3 | D. | x≥1且x≠3 |
13.|-2015|的相反数是( )
| A. | 2015 | B. | -2015 | C. | $\frac{1}{2015}$ | D. | -$\frac{1}{2015}$ |
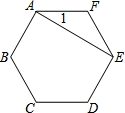 如图,在正六边形ABCDEF中,连接AE,则tan∠1=$\frac{\sqrt{3}}{3}$.
如图,在正六边形ABCDEF中,连接AE,则tan∠1=$\frac{\sqrt{3}}{3}$.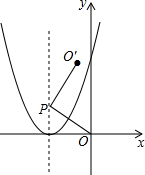 如图,在平面直角坐标系中,点P是抛物线y=x2+4x+4对称轴上的任意一点,将线段OP绕点P逆时针方向旋转90°得到线段PO′.若点O′落在抛物线上,则点P的坐标是(-2,2)或(-2,-1).
如图,在平面直角坐标系中,点P是抛物线y=x2+4x+4对称轴上的任意一点,将线段OP绕点P逆时针方向旋转90°得到线段PO′.若点O′落在抛物线上,则点P的坐标是(-2,2)或(-2,-1).