题目内容
3．解不等式组$\left\{\begin{array}{l}{2x-3＞5}\\{\frac{2+x}{3}-1≤2}\end{array}\right.$．分析 分别求出各不等式的解集，再求出其公共解集即可．
解答 解：$\left\{\begin{array}{l}{2x-3＞5①}\\{\frac{2+x}{3}-1≤2②}\end{array}\right.$
解不等式①得 x＞4．
解不等式②得 x≤7．
∴原不等式组解集为4＜x≤7．
点评 本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
优生乐园系列答案
相关题目
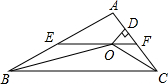如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC交AB于E，交AC于F，过点O作OD⊥AC于D．下列四个结论：①∠BOC=90°+$\frac{1}{2}$∠A； ②EF=BE+CF；③设OD=m，AE+AF=n，则S△AEF=$\frac{1}{2}$mn； ④EF是△ABC的中位线．其中正确的结论是①②③．
11．计算a6b2÷（ab）2的结果是（ ）
| A． | a3 | B． | a4 | C． | a3b | D． | a4b |
15．在$\frac{\sqrt{1-x}}{x}$中，x的取值范围为（ ）
| A． | x≥1且x≠0 | B． | x≠0 | C． | x≤1且x≠0 | D． | x≤1 |
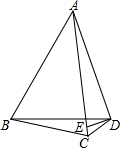如图，四边形ABCD中，AC、BD是对角线，AB=AC，∠ABD=60°，过D作ED⊥AD，交AC于点E，恰有DE平分∠BDC．试判断线段CD、BD与AC之间有怎样的数量关系？并证明你的结论．