题目内容
14.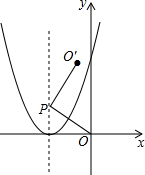 如图,在平面直角坐标系中,点P是抛物线y=x2+4x+4对称轴上的任意一点,将线段OP绕点P逆时针方向旋转90°得到线段PO′.若点O′落在抛物线上,则点P的坐标是(-2,2)或(-2,-1).
如图,在平面直角坐标系中,点P是抛物线y=x2+4x+4对称轴上的任意一点,将线段OP绕点P逆时针方向旋转90°得到线段PO′.若点O′落在抛物线上,则点P的坐标是(-2,2)或(-2,-1).
分析 过O′作O′H⊥x轴于H,过P作PN⊥O′H于N,则四边形PMHN是矩形,得到PN=MH,PM=NH,由线段OP绕点P逆时针方向旋转90°得到线段PO,再通过三角形全等得到PM=PN,OM=O′N,根据函数图形上点的特征表示出点的坐标,代入二次函数的解析式即可得到结果.
解答 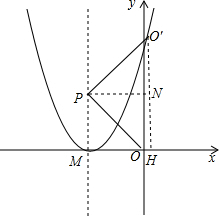 解:过O′作O′H⊥x轴于H,过P作PN⊥O′H于N,
解:过O′作O′H⊥x轴于H,过P作PN⊥O′H于N,
设抛物线与轴交于M,则四边形PMHN是矩形,
∴PN=MH,PM=NH,
∵线段OP绕点P逆时针方向旋转90°得到线段PO′,
∴PO=PO′,∠OPO′=90°,
在△PMO与△PNO′中,
$\left\{\begin{array}{l}{∠PMO=∠PNO′}\\{∠MPO=∠NPO′}\\{PO=PO′}\end{array}\right.$,
∴△PMO≌△PNO′,
∴PM=PN,OM=O′N,
点P是抛物线y=x2+4x+4对称轴上一点,
∵抛物线y=x2+4x+4的对称轴是x=-2,
∴设P(-2,m),
∴PM=PN=m,OM=O′N=2,
∴O′(m-2,m+2),
∵O′在抛物线上,
∴m+2=(m-2)2+4(m-2)+4,
解得m=2,m=-1,
∴P(-2,2)或P(-2,-1).
故答案为:(-2,2)或(-2,-1).
点评 本题考查了坐标与图形的变换-旋转,全等三角形的判定与性质,函数图形上点的特征,正确的画出图形是解题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
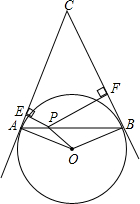 已知:如图所示,P为直径为2的⊙O内一定点,且PO=$\frac{\sqrt{2}}{2}$,线段AB为过点P的任一弦,且它所对的圆心角∠AOB=2θ,再过点A和B作⊙O的切线交于C,设P到AC、BC的距离分别为a、b.求证:a、b是方程2x2-(2ABsinθ)x+sin2θ=0的两个根.
已知:如图所示,P为直径为2的⊙O内一定点,且PO=$\frac{\sqrt{2}}{2}$,线段AB为过点P的任一弦,且它所对的圆心角∠AOB=2θ,再过点A和B作⊙O的切线交于C,设P到AC、BC的距离分别为a、b.求证:a、b是方程2x2-(2ABsinθ)x+sin2θ=0的两个根.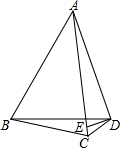 如图,四边形ABCD中,AC、BD是对角线,AB=AC,∠ABD=60°,过D作ED⊥AD,交AC于点E,恰有DE平分∠BDC.试判断线段CD、BD与AC之间有怎样的数量关系?并证明你的结论.
如图,四边形ABCD中,AC、BD是对角线,AB=AC,∠ABD=60°,过D作ED⊥AD,交AC于点E,恰有DE平分∠BDC.试判断线段CD、BD与AC之间有怎样的数量关系?并证明你的结论.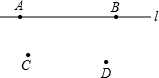 如图,在一条笔直的高速公路I上有A、B两点,点C、D表示两个村庄,相关部门计划在高速公路的AB路段上修建一个收费站E,使得此收费站E到C、D两村庄的距离相等,请你在图中画出收费站E的位置.(保留作图痕迹,不要求写作法)
如图,在一条笔直的高速公路I上有A、B两点,点C、D表示两个村庄,相关部门计划在高速公路的AB路段上修建一个收费站E,使得此收费站E到C、D两村庄的距离相等,请你在图中画出收费站E的位置.(保留作图痕迹,不要求写作法)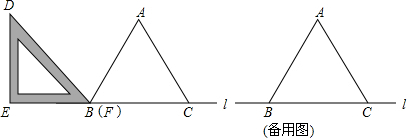
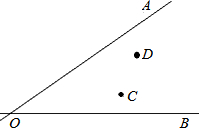 如图所示,107国道OA和320国道OB在某巿相交于O点,在∠AOB的内部有工厂C和D,现要建一个货站P,使P到OA和OB的距离相等,且使PC=PD,用尺规作出P点的位置.(不写作法,保留作图痕迹,写出结论)
如图所示,107国道OA和320国道OB在某巿相交于O点,在∠AOB的内部有工厂C和D,现要建一个货站P,使P到OA和OB的距离相等,且使PC=PD,用尺规作出P点的位置.(不写作法,保留作图痕迹,写出结论)