题目内容
1.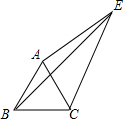 如图,△ABC是等边三角形,点E为△ABC,∠AEC=30°,AE=3,CE=4,则BE=5.
如图,△ABC是等边三角形,点E为△ABC,∠AEC=30°,AE=3,CE=4,则BE=5.
分析 如图将线段CE绕点C顺时针旋转60°得到线段CD,连接ED,则△CDE是等边三角形.先证明△ACD≌△BCE,得到AD=BE,在Rt△ADE中,由勾股定理,
可得AD=$\sqrt{A{E}^{2}+E{D}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5.
解答 解:如图将线段CE绕点C顺时针旋转60°得到线段CD,连接ED,则△CDE是等边三角形.
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
由旋转的性质可得:
CE=CD,∠DCE=60°,
∴∠DCE+∠ACD=∠ACB+∠ACD,
即∠ACD=∠BCE,
在△ACE≌△BCD中,
$\left\{\begin{array}{l}{CA=CB}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE,
∴AD=BE,
∵△DCE是等边三角形,
∴∠CDE=60°,DC=DE=4,
∵∠ADC=30°,
∴∠ADC+∠CDE=90°,
∴∠AED=90°,∵AE=3,ED=4,
在Rt△ADE中,由勾股定理,
可得AD=$\sqrt{A{E}^{2}+E{D}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴BE=AD=5.
故答案为5.
点评 本题主要考查旋转的性质、等边三角形的性质、全等三角形的判定与性质及勾股定理的应用,解题的关键是利用旋转的方法添加辅助线,构造全等三角形以及直角三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
6. 如图,点C是⊙O上一点,⊙O的半径为$2\sqrt{2}$,D、E分别是弦AC、BC上一动点,且OD=OE=$\sqrt{2}$,则AB的最大值为( )
如图,点C是⊙O上一点,⊙O的半径为$2\sqrt{2}$,D、E分别是弦AC、BC上一动点,且OD=OE=$\sqrt{2}$,则AB的最大值为( )
 如图,点C是⊙O上一点,⊙O的半径为$2\sqrt{2}$,D、E分别是弦AC、BC上一动点,且OD=OE=$\sqrt{2}$,则AB的最大值为( )
如图,点C是⊙O上一点,⊙O的半径为$2\sqrt{2}$,D、E分别是弦AC、BC上一动点,且OD=OE=$\sqrt{2}$,则AB的最大值为( )| A. | $2\sqrt{6}$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | $4\sqrt{2}$ |
13.已知32m=8n,则m、n满足的关系正确的是( )
| A. | 4m=n | B. | 5m=3n | C. | 3m=5n | D. | m=4n |
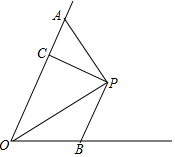 已知:如图所示,点P为∠AOB的平分线上一点,PC⊥OA于C,∠OAP+∠OBP=180°,求证:OA+OB=2OC.
已知:如图所示,点P为∠AOB的平分线上一点,PC⊥OA于C,∠OAP+∠OBP=180°,求证:OA+OB=2OC.