题目内容
6. 如图,点C是⊙O上一点,⊙O的半径为$2\sqrt{2}$,D、E分别是弦AC、BC上一动点,且OD=OE=$\sqrt{2}$,则AB的最大值为( )
如图,点C是⊙O上一点,⊙O的半径为$2\sqrt{2}$,D、E分别是弦AC、BC上一动点,且OD=OE=$\sqrt{2}$,则AB的最大值为( )| A. | $2\sqrt{6}$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | $4\sqrt{2}$ |
分析 先判断出OD⊥AC、OE⊥BC时∠ACB最大,从而得到AB最大,连接OC,根据直角三角形30°角所对的直角边等于斜边的一半求出∠ACO=30°,再根据垂径定理和勾股定理求出AC,然后求出∠ACB=60°,再求出AC=BC,从而得到△ABC是等边三角形,最后根据等边三角形的性质可得AB=AC.
解答 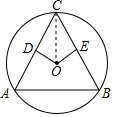 解:如图,当OD⊥AC、OE⊥BC时∠ACB最大,AB最大,
解:如图,当OD⊥AC、OE⊥BC时∠ACB最大,AB最大,
连接OC,
∵⊙O的半径为2$\sqrt{2}$,OD=$\sqrt{2}$,
∴∠ACO=30°,
∴AC=2CD=2$\sqrt{O{C}^{2}-O{D}^{2}}$=2$\sqrt{(2\sqrt{2})^{2}-(\sqrt{2})^{2}}$=2$\sqrt{6}$,
同理可得∠BCO=30°,
∴∠ACB=60°,
∵OD=OE,OD⊥AC、OE⊥BC,
∴AC=BC,
∴△ABC是等边三角形,
∴AB=AC=2$\sqrt{6}$,
即AB的最大值为2$\sqrt{6}$.
故选A.
点评 本题考查了垂径定理,等边三角形的判定与性质,勾股定理,熟练掌握圆的性质并判断出AB取得最大值的情况是解题的关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
11.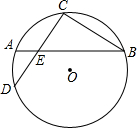 如图,弦AB、CD交于点E,∠C=90°,tanB=$\frac{2}{3}$,若AE=4,则DE的长为( )
如图,弦AB、CD交于点E,∠C=90°,tanB=$\frac{2}{3}$,若AE=4,则DE的长为( )
 如图,弦AB、CD交于点E,∠C=90°,tanB=$\frac{2}{3}$,若AE=4,则DE的长为( )
如图,弦AB、CD交于点E,∠C=90°,tanB=$\frac{2}{3}$,若AE=4,则DE的长为( )| A. | 2$\sqrt{13}$ | B. | 8 | C. | 2$\sqrt{14}$ | D. | 5 |
16.已知a+b=5,ab=3,则a2+b2=( )
| A. | 19 | B. | 28 | C. | 25 | D. | 22 |

 如图,长方形ABCD中,AB=4,BC=3,将其沿直线MN折叠,使点C与点A重合,求CN的长.
如图,长方形ABCD中,AB=4,BC=3,将其沿直线MN折叠,使点C与点A重合,求CN的长.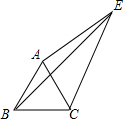 如图,△ABC是等边三角形,点E为△ABC,∠AEC=30°,AE=3,CE=4,则BE=5.
如图,△ABC是等边三角形,点E为△ABC,∠AEC=30°,AE=3,CE=4,则BE=5.
 -5a=a2+3a-2
-5a=a2+3a-2