题目内容
2.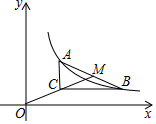 如图,已知点A(2,n),B(6,m)是双曲线y=$\frac{6}{x}$上的两点,分别过点A,B 作x 轴,y 轴的垂线交于点C,OC 的延长线与AB交于点M,则tan∠MCB=$\frac{1}{2}$.
如图,已知点A(2,n),B(6,m)是双曲线y=$\frac{6}{x}$上的两点,分别过点A,B 作x 轴,y 轴的垂线交于点C,OC 的延长线与AB交于点M,则tan∠MCB=$\frac{1}{2}$.
分析 根据反比例函数图象上点的坐标特征求得A(2,3),B(6,1),即可求得C(2,1),进一步求得tan∠1=$\frac{1}{2}$,由BC∥x轴,得出∠MCB=∠1,即可求得tan∠MCB=$\frac{1}{2}$.
解答 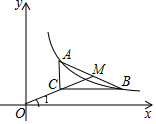 解:∵点A(2,n),B(6,m)是双曲线y=$\frac{6}{x}$上的两点,
解:∵点A(2,n),B(6,m)是双曲线y=$\frac{6}{x}$上的两点,
∴2n=6m=6,
∴n=3,m=1,
∴A(2,3),B(6,1),
∴C(2,1),
∴tan∠1=$\frac{1}{2}$,
∵BC∥x轴,
∴∠MCB=∠1,
∴tan∠MCB=$\frac{1}{2}$.
故答案为$\frac{1}{2}$.
点评 本题考查了反比例函数图象上点的坐标特征,求得C的坐标上解题的关键.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
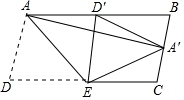 如图,将平行四边形纸片ABCD折叠,使得点D落在AB边上的D'处,折痕为AE.再将△AD'E翻折,点A恰好落在BC的中点A'处,连结AA',若AD=2,则线段AA'的长为$\sqrt{15}$.
如图,将平行四边形纸片ABCD折叠,使得点D落在AB边上的D'处,折痕为AE.再将△AD'E翻折,点A恰好落在BC的中点A'处,连结AA',若AD=2,则线段AA'的长为$\sqrt{15}$.
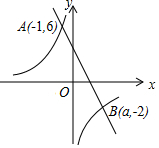 如图,在直角坐标系xoy中,一次函数y1=k1x+b的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(-1,6)、B(a,-2)两点.
如图,在直角坐标系xoy中,一次函数y1=k1x+b的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(-1,6)、B(a,-2)两点.