题目内容
13.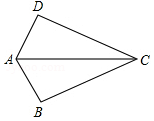 如图,已知AB=AD,那么添加下列一个条件后,能判定△ABC≌△ADC的是( )
如图,已知AB=AD,那么添加下列一个条件后,能判定△ABC≌△ADC的是( )| A. | AC=AC | B. | ∠BAC=∠DAC | C. | ∠BCA=∠DCA | D. | ∠B=∠D |
分析 要判定△ABC≌△ADC,已知AB=AD,AC是公共边,具备了两组边对应相等,故添加CB=CD、∠BAC=∠DAC、∠B=∠D=90°后可分别根据SSS、SAS、HL能判定△ABC≌△ADC,而添加∠BCA=∠DCA后则不能.
解答 解:A、添加AC=AC,根据SS,不能判定△ABC≌△ADC,故本选项错误;
B、添加∠BAC=∠DAC,根据SAS,能判定△ABC≌△ADC,故本选项正确;
C、添加∠BCA=∠DCA时,根据SSA不能判定△ABC≌△ADC,故本选项错误;
D、添加∠B=∠D,根据SSA不能判定△ABC≌△ADC,故本选项错误;
故选:B.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
8.某电动自行车厂本周计划每天生产250辆电动自行车,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(增加的车辆数记作正数,减少的车辆数记作负数)
根据记录:
(1)本周内每天分别生产了多少辆电动自行车?
(2)本周是否完成了周计划?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
(1)本周内每天分别生产了多少辆电动自行车?
(2)本周是否完成了周计划?
18.下列因式分解正确的是( )
| A. | a2+4=(a+2)2 | B. | a2-2a+4=(a-2)2 | C. | x3-4x2=x2(x-4) | D. | 1-4x2=(1+4x)(1-4x) |
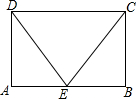 如图,在矩形ABCD中,E分别是AB的一点,s△CDE=2SAEC,求证:△BEC≌△ADE.
如图,在矩形ABCD中,E分别是AB的一点,s△CDE=2SAEC,求证:△BEC≌△ADE. 如图,在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(-4,0),以AB为边作正方形ABCD,连接OD,DB.则△DOB的面积是14.
如图,在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(-4,0),以AB为边作正方形ABCD,连接OD,DB.则△DOB的面积是14.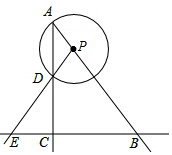 Rt△ABC,∠ACB=90°,AC=4,BC=3,P是射线AB上的一个动点,以P为圆心,PA为半径的圆P与射线AC的另一个交点为D,直线PD交BC于点E.
Rt△ABC,∠ACB=90°,AC=4,BC=3,P是射线AB上的一个动点,以P为圆心,PA为半径的圆P与射线AC的另一个交点为D,直线PD交BC于点E.