题目内容
4.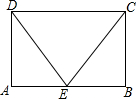 如图,在矩形ABCD中,E分别是AB的一点,s△CDE=2SAEC,求证:△BEC≌△ADE.
如图,在矩形ABCD中,E分别是AB的一点,s△CDE=2SAEC,求证:△BEC≌△ADE.
分析 由矩形的性质得出∠A=∠B=90°,AD=BC,AB=CD,由三角形的面积关系得出CD=2AE,AB=2AE,证出AE=BE,由SAS证明:△BEC≌△ADE即可.
解答 证明:∵四边形ABCD是矩形,
∴∠A=∠B=90°,AD=BC,AB=CD,
∵S△CDE=2SAEC,
∴CD=2AE,
∴AB=2AE,
∴AE=BE,
在△BEC和△ADE中,$\left\{\begin{array}{l}{BC=AD}&{\;}\\{∠B=∠A}&{\;}\\{BE=AE}&{\;}\end{array}\right.$,
∴△BEC≌△ADE(SAS).
点评 本题考查了矩形的性质、全等三角形的判定与性质;熟练掌握矩形的性质,证出AE=BE是解决问题的关键.

练习册系列答案
相关题目
14.已知a2-2a-1=0,则a4-2a3-2a+1等于( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
15.抛物线y=-4x2+3的对称轴及顶点坐标分别是( )
| A. | y轴,(0,-4) | B. | x=3,(0,4) | C. | x轴,(0,0) | D. | y轴,(0,3) |
19. 某几何体的主视图、左视图和俯视图分别如图,则该几何体的全面积是( )
某几何体的主视图、左视图和俯视图分别如图,则该几何体的全面积是( )
 某几何体的主视图、左视图和俯视图分别如图,则该几何体的全面积是( )
某几何体的主视图、左视图和俯视图分别如图,则该几何体的全面积是( )| A. | 14π | B. | 16π | C. | 18π | D. | 24π |
13.总投资约160亿元,线路全长约29.06km的合肥地铁一号线已于2016年12月31日正式运营,这标志着合肥从此进入了地铁时代,将160亿用科学记数法表示为( )
| A. | 160×108 | B. | 16×109 | C. | 1.6×1010 | D. | 1.6×1011 |
13.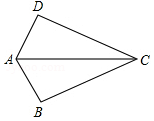 如图,已知AB=AD,那么添加下列一个条件后,能判定△ABC≌△ADC的是( )
如图,已知AB=AD,那么添加下列一个条件后,能判定△ABC≌△ADC的是( )
 如图,已知AB=AD,那么添加下列一个条件后,能判定△ABC≌△ADC的是( )
如图,已知AB=AD,那么添加下列一个条件后,能判定△ABC≌△ADC的是( )| A. | AC=AC | B. | ∠BAC=∠DAC | C. | ∠BCA=∠DCA | D. | ∠B=∠D |
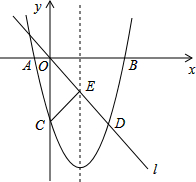 如图,在平面直角坐标系中,已知抛物线y=ax2+bx-8与x轴交于A,B两点,与y轴交于点C,直线L经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0),(6,-8).
如图,在平面直角坐标系中,已知抛物线y=ax2+bx-8与x轴交于A,B两点,与y轴交于点C,直线L经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0),(6,-8).