题目内容
3.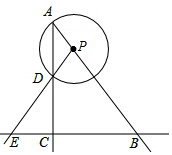 Rt△ABC,∠ACB=90°,AC=4,BC=3,P是射线AB上的一个动点,以P为圆心,PA为半径的圆P与射线AC的另一个交点为D,直线PD交BC于点E.
Rt△ABC,∠ACB=90°,AC=4,BC=3,P是射线AB上的一个动点,以P为圆心,PA为半径的圆P与射线AC的另一个交点为D,直线PD交BC于点E.(1)AB=5;
(2)求证:PB=PE;
(3)若AP=2,求ED,DC的长;
(4)若圆P与边BC没有公共点,直接写出AP的取值范围.
分析 (1)直接利用勾股定理得出AB的长;
(2)利用等腰三角形的性质得出∠A=∠PDA,进而得出∠PBE=∠PEB,求出即可;
(2)由相似三角形的判定定理得出△ABC∽△DEC,再根据锐角三角函数的定义即可得出结论;
(4)直接利用圆P与边BC相切前以及A,C,B共圆后分别得出AP的取值范围.
解答  (1)解:∵∠ACB=90°,AC=4,BC=3,
(1)解:∵∠ACB=90°,AC=4,BC=3,
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
故答案为:5;
(2)证明:如图1,∵PA=PD,
∴∠A=∠PDA,
∵∠EDC=∠PDA,∴∠A=∠EDC,
∵AC⊥BC,
∴∠PBE=∠PEB,
∴PB=PE;
(3)解:如图1,
∵AP=DP,
∴∠PAD=∠PDA.
∴∠PAD=∠CDE.
∵∠ACB=∠DCE=90°,
∴△ABC∽△DEC.
∴∠ABC=∠DEC,$\frac{BC}{EC}$=$\frac{AB}{DE}$=$\frac{AC}{DC}$.
∴PB=PE.
Rt△ABC中,∠ABC=90°,
∵AC=4,BC=3,
∴AB=5.
∵AP=2,
∴PB=PE=3,DE=1,
∴$\frac{4}{DC}$=$\frac{5}{1}$,
解得:CD=$\frac{4}{5}$;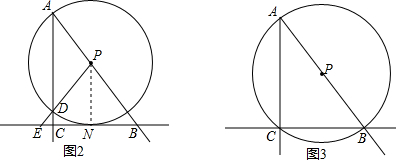
(4)如图2所示:
当⊙P与直线BC相切,切点为N,
连接PN,则PN⊥BC与点N,
∵∠PNB=∠ACB=90°,
∴AC∥PN,
∴△ACB∽△PNB,
∴$\frac{PN}{AC}$=$\frac{PB}{AB}$,
设⊙P的半径为AP=x,
∴$\frac{x}{4}$=$\frac{5-x}{5}$,
解得:x=$\frac{20}{9}$,
∴当0<AP<$\frac{20}{9}$时,圆P与边BC没有公共点,
如图3,当A,C,B三点共圆,则AB是直径,此时AP=$\frac{1}{2}$AB=$\frac{5}{2}$,
故当$\frac{5}{2}$<AP时,圆P与边BC没有公共点,
综上所述,当0<AP<$\frac{20}{9}$时或当$\frac{5}{2}$<AP时,圆P与边BC没有公共点.
点评 本题考查的是圆的综合题,涉及到相似三角形的判定与性质、切线的性质等知识,得出△ABC∽△DEC是解题关键.

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案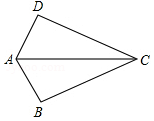 如图,已知AB=AD,那么添加下列一个条件后,能判定△ABC≌△ADC的是( )
如图,已知AB=AD,那么添加下列一个条件后,能判定△ABC≌△ADC的是( )| A. | AC=AC | B. | ∠BAC=∠DAC | C. | ∠BCA=∠DCA | D. | ∠B=∠D |
| A. | 1,2,3,4 | B. | $\sqrt{2}$,$\sqrt{3}$,1,$\sqrt{6}$ | C. | 2,4,6,8 | D. | 2,5,3,10 |
| A. | x=1 | B. | x=-1 | C. | x=1或x=-1 | D. | 不能确定 |
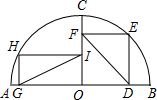 如图,C是以点O为圆心,AB为直径的半圆上一点,且CO⊥AB,在OC两侧分别作矩形OGHI和正方形ODEF,且点I,F在OC上,点H,E在半圆上,可证:IG=FD.小云发现连接图中已知点得到两条线段,便可证明IG=FD.
如图,C是以点O为圆心,AB为直径的半圆上一点,且CO⊥AB,在OC两侧分别作矩形OGHI和正方形ODEF,且点I,F在OC上,点H,E在半圆上,可证:IG=FD.小云发现连接图中已知点得到两条线段,便可证明IG=FD.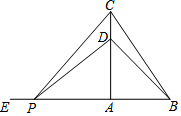 如图,在△ABC中,∠BAC=90°,AB=3 cm,BC=5 cm,点D在线段AC上,且CD=1 cm,动点P从BA的延长线上距A点5 cm的E点出发,以每秒2 cm的速度沿射线EA的方向运动了t秒.
如图,在△ABC中,∠BAC=90°,AB=3 cm,BC=5 cm,点D在线段AC上,且CD=1 cm,动点P从BA的延长线上距A点5 cm的E点出发,以每秒2 cm的速度沿射线EA的方向运动了t秒.