题目内容
13.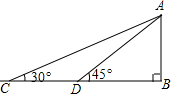 如图,某数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端点A的仰角为30°,再向旗杆的方向前进12米,到达点D处(C,D,B三点在同一直线上),又测得旗杆顶端点A的仰角为45°,请计算旗杆AB的高度.(结果保留根号)
如图,某数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端点A的仰角为30°,再向旗杆的方向前进12米,到达点D处(C,D,B三点在同一直线上),又测得旗杆顶端点A的仰角为45°,请计算旗杆AB的高度.(结果保留根号)
分析 设AB为x米,根据正切的定义用x表示出BD、BC,根据题意列出方程,解方程即可.
解答 解:设AB为x米,
∵∠ADB=45°,
∴BD=AB=x,
在Rt△ACB中,tan∠ACB=$\frac{AB}{BC}$,
∴BC=$\sqrt{3}$x,
由题意得,$\sqrt{3}$x-x=12,
解得,x=6$\sqrt{3}$+6,
答:旗杆AB的高度为(6$\sqrt{3}$+6)米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
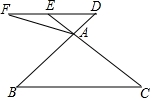 如图,在△ABC中,点D是BA边延长线上一点,过点D作DE∥BC,交CA延长线于点E,点F是DE延长线上一点,连接AF.
如图,在△ABC中,点D是BA边延长线上一点,过点D作DE∥BC,交CA延长线于点E,点F是DE延长线上一点,连接AF.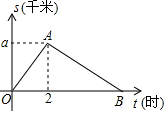 某单位举行“健康人生”徒步走活动,某人从起点体育村沿建设路到市生态园,再沿原路返回,设此人离开起点的路程s(千米)与走步时间t(小时)之间的函数关系如图所示,其中从起点到市生态园的平均速度是4千米/小时,用2小时,根据图象提供信息,解答下列问题.
某单位举行“健康人生”徒步走活动,某人从起点体育村沿建设路到市生态园,再沿原路返回,设此人离开起点的路程s(千米)与走步时间t(小时)之间的函数关系如图所示,其中从起点到市生态园的平均速度是4千米/小时,用2小时,根据图象提供信息,解答下列问题.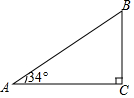 如图,某山坡坡长AB为110米,坡角(∠A)为34°,求坡高BC及坡宽AC.(结果精确到0.1米)
如图,某山坡坡长AB为110米,坡角(∠A)为34°,求坡高BC及坡宽AC.(结果精确到0.1米)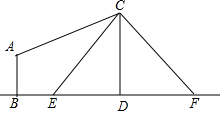 如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=$\sqrt{3}$米,BE=3米,求拉线CE的长.
如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=$\sqrt{3}$米,BE=3米,求拉线CE的长.