题目内容
14．小明对自己上学路线的长度进行了10次测量，得到10个数据x1、x2、…、x10．已知x1+x2+…+x10=5432m，则当代数式（x-x1）2+（x-x2）2+…+（x-x10）2取得最小值时，x的值为543.2m．分析 设y=（x-x1）2+（x-x2）2+（x-x3）2+…+（x-x10）2，化为以x为自变量的二次函数的形式，根据二次函数的性质求出最小值．
解答 解：设y=（x-x1）2+（x-x2）2+（x-x3）2+…+（x-x10）2
=x2-2xx1+x12+x2-2xx2+x22+x2-2xx3+x32+…+x2-2xx10+x102
=10x2-2（x1+x2+x3+…+x10）x+（x12+x22+x32+…+x102），
=10x2-2×5432x+（x12+x22+x32+…+x202），
x=$\frac{10864}{20}$=543.2m时，代数式（x-x1）2+（x-x2）2+…+（x-x10）2取得最小值，
故答案为：543.2．
点评 本题考查的是方差的概念和二次函数的性质，掌握二次函数的最值的求法是解题的关键．
练习册系列答案
相关题目
5．在直角坐标系中，点P（-3，6）关于原点对称的点是（ ）
| A． | （-3，-6） | B． | （3，6） | C． | （3，-6） | D． | （6，-3） |
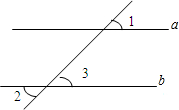仔细想一想，完成下面的推理过程