题目内容
2.已知$\frac{a+2b}{3}$=$\frac{b+3c}{4}$=$\frac{c+5a}{5}$,则a:b:c=25:34:30.分析 根据等式的性质,可用c表示a,用c表示b,根据比的性质,可得答案.
解答 解:都乘以60,得
20a+40b=15b+45c=12c+60a.
$\left\{\begin{array}{l}{20a+40b=15b+45c}\\{20a+40b=12c+60a}\\{15b+45c=12c+60a}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{5}{6}c}\\{b=\frac{17}{15}c}\end{array}\right.$,
a:b:c=($\frac{5}{6}$c):($\frac{17}{15}$c):c=25:34:30,
故答案为:25:34:30.
点评 本题考查了比例的性质,利用比例的性质得出c表示a,c表示b是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.计算(-48)÷(-12)的结果是( )
| A. | 4 | B. | $\frac{1}{4}$ | C. | -4 | D. | -$\frac{1}{4}$ |
17.等腰三角形的周长为13,各边长均为整数,则这样的三角形有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 无数个 |
 已知直线y=$\frac{\sqrt{3}}{3}$x与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,且点A的横坐标为$\sqrt{3}$
已知直线y=$\frac{\sqrt{3}}{3}$x与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,且点A的横坐标为$\sqrt{3}$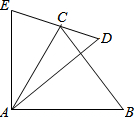 如图所示,AE=AC,AD=AB,∠EAC=∠DAB,求证:∠D=∠B.
如图所示,AE=AC,AD=AB,∠EAC=∠DAB,求证:∠D=∠B.