题目内容
9.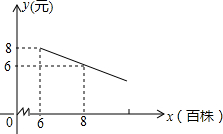 某花店计划用100个花盆培育一种花卉,用于国庆销售,已知花店从批发市场购进花苗的单价为y(元)和数量x(百株)之间的关系如图所示(其中x≥6),根据以往经验,每年的花卉供不应求,但若每个花盆培育6株,每株的销售单价为26元,每个花盆每增加1株,每株的销售单价就减少2元.
某花店计划用100个花盆培育一种花卉,用于国庆销售,已知花店从批发市场购进花苗的单价为y(元)和数量x(百株)之间的关系如图所示(其中x≥6),根据以往经验,每年的花卉供不应求,但若每个花盆培育6株,每株的销售单价为26元,每个花盆每增加1株,每株的销售单价就减少2元.(1)试求单价与数量之间的函数关系式;
(2)若要使每个花盆的销售总额P(元)最高,每个花盆应该培育多少株花卉?
(3)若要使花店的总利润(元)最大,每盆又应该培育多少株花卉?最大利润是多少?
注:总利润=(每株售价-每株单价)×总数量.
分析 (1)根据直线经过的两点的坐标利用待定系数法确定一次函数的解析式即可;
(2)设每个花盆应该培育a株花卉,则每株花卉的售价为:[26-2(a-6)]元,由数量×单价=总价建立p与a的关系式即可;
(3)根据(1)结论分别求出求出每株的进价,由利润=销售总额-进价总额就可以得出结论.
解答 解:(1)设单价与之间的函数关系式为y=kx+b,
∵经过点(6,8)和(8,6),
∴$\left\{\begin{array}{l}{6k+b=8}\\{8k+b=6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=14}\end{array}\right.$,
∴单价与之间的函数关系式为y=-x+14;
(2)设每个花盆应该培育a株花卉,则每株花卉的售价为:[26-2(a-6)]元,由题意,得
p=a[26-2(a-6)],
=-2(a-9.5)2+$\frac{361}{2}$,
∵a为整数,
∴a=9或10时,p最大=180.
答:每个花盆应该培育9株或10株花卉;
(3)每个花盆培育a株,100个花盆共100a,
∴y=-a+14.
∴W=[26-2(a-6)-(-a+14)]×100a=-100a2+2400a=-100(a-12)2+14400,
∴每盆应该培育12株花卉,最大利润是14400元.
点评 本题考查了二次函数的解析式的运用,二次函数的性质的运用,利润率问题的数量关系的运用,解答时求出二次函数的关系式是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知△ABC:
如图,已知△ABC: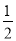 BC,连结DE,CF。
BC,连结DE,CF。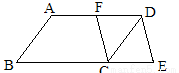
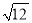 ︱+(
︱+(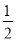 )-2;
)-2;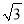 x-
x-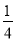 = 0.
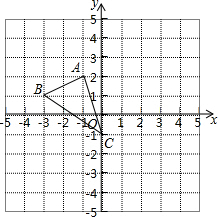
= 0.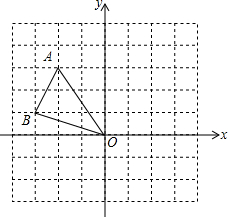 如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别为A(-2,3)、B(-3,1).
如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别为A(-2,3)、B(-3,1). 已知:在平面直角坐标系xoy中,抛物线y=ax2+bx+c与直线y=mx+n相交于
已知:在平面直角坐标系xoy中,抛物线y=ax2+bx+c与直线y=mx+n相交于