题目内容
3.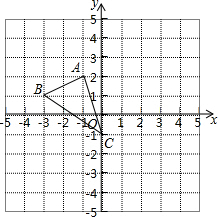 如图,已知△ABC:
如图,已知△ABC:(1)AC的长等于$\sqrt{10}$;
(2)若将△ABC向右平移2个单位得到△A′B′C′,则A点的对应点A′的坐标是(1,2);
(3)若将△ABC绕点C按顺时针方向旋转90°后得到△A1B1C1,则A点对应点A1的坐标是(3,0).
分析 (1)直接利用勾股定理求出AC的长即可;
(2)利用平移的性质得出对应点位置进而得出答案;
(3)利用旋转的性质得出对应点位置进而得出答案.
解答  解:(1)AC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$;
解:(1)AC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$;
故答案为:$\sqrt{10}$;
(2)如图所示:△A′B′C′即为所求,
A点的对应点A′的坐标为:(1,2);
故答案为:(1,2);
(3)如图所示:△A1B1C1,即为所求;
A点对应点A1的坐标是:(3,0).
故答案为:(3,0).
点评 此题主要考查了勾股定理以及平移变换和旋转变换,正确根据题意得出对应点位置是解题关键.

练习册系列答案
相关题目
2.观察如图图形,图(1)中有3个三角形,图(2)中有5个三角形,图(3)中有7个三角形,…若依此规律下去,则第2014个图形中三角形的个数是( )


| A. | 4028 | B. | 4029 | C. | 4030 | D. | 4031 |
 B.
B. C.
C. D.
D.
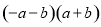 B.
B. 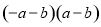
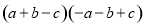 D.
D. 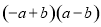
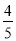 ,求BF的长.
,求BF的长.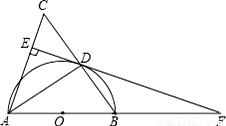
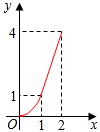
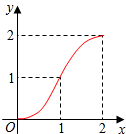
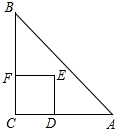 如图,Rt△ABC中,∠C=90°,AC=BC=2,正方形CDEF的顶点D、F分别在AB、BC边上,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象能表示y与x之间的函数关系的是( )
如图,Rt△ABC中,∠C=90°,AC=BC=2,正方形CDEF的顶点D、F分别在AB、BC边上,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象能表示y与x之间的函数关系的是( )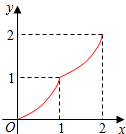

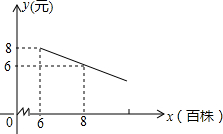 某花店计划用100个花盆培育一种花卉,用于国庆销售,已知花店从批发市场购进花苗的单价为y(元)和数量x(百株)之间的关系如图所示(其中x≥6),根据以往经验,每年的花卉供不应求,但若每个花盆培育6株,每株的销售单价为26元,每个花盆每增加1株,每株的销售单价就减少2元.
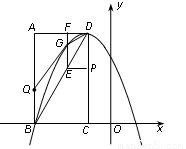
某花店计划用100个花盆培育一种花卉,用于国庆销售,已知花店从批发市场购进花苗的单价为y(元)和数量x(百株)之间的关系如图所示(其中x≥6),根据以往经验,每年的花卉供不应求,但若每个花盆培育6株,每株的销售单价为26元,每个花盆每增加1株,每株的销售单价就减少2元.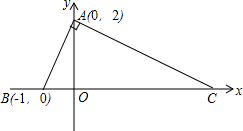 如图,平面直角坐标系中,AB⊥AC,
如图,平面直角坐标系中,AB⊥AC,