题目内容
18.城南农业园果蔬公司新培育了一种葡萄,决定在市场上进行试推销,已知试推销期间每天需固定支出各种费用(场地费、推销员工资等)600元,该葡萄成本价为每千克5元,经测算若按成本价5元/千克进行推销时,每天可销售1440千克,若每千克每提高1元,每天就少销售120千克.为便于测算,每千克葡萄的售价x(元)只取整数.设该公司的日净收入为y元.(日净收入=销售收入-成本-日固定支出)(1)写出y与x的函数关系式,并指出x的取值范围;
(2)公司若要使得日净收入最大,则每千克葡萄的售价应定为多少元?此时日净收入是多少?
(3)若要求日净收入不低于3000元,依据函数的图象确定每千克葡萄的售价应定在什么范围?
分析 (1)根据日净收入=(每个售价-每个成本)×销售量-固定支出费用,进而得出即可;
(2)根据配方法求出二次函数最值即可;
(3)根据(2)中所求以及要求日净收入不低于3000元,即y≥3000,求出x的取值范围即可
解答 解:(1)∵按成本价5元/个进行推销,每天可销售1440个,若每个提高1元,每天就少销售120个,每个产品的售价x(元)只取整数,
设该团队的日净收入为y元,
∴y=[1440-120(x-5)](x-5)-600
=-120x2+2640x-10800,(5≤x≤17且x为整数);
(2)由(1)得出:
y=-120x2+2640x-10800
=-120(x-11) 2+3720,
当x=11时,y最大=3720.
答:当每个产品售价为11元时,日净收入最大,为3720元.
(3)由于-120<0,抛物线开口向下,x=11为对称轴,x≤11递增,x≥11,函数递减,
若要求日净收入不低于3000元,即y≥3000.
所以(x-11)2≤6,因为x为整数,所以9≤x≤13.
所以每个产品的售价应定在9元/千克到13元/千克之间,包括9元/千克和13元/千克.
点评 此题主要考查了二次函数的应用以及配方法求二次函数最值问题以及不等式的应用,正确根据已知得出y与x的函数关系式是解题关键.

练习册系列答案
相关题目
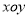 中,已知点
中,已知点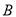 (-3,4)关于
(-3,4)关于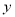 轴的对称点为
轴的对称点为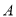 .
. 点的坐标;
点的坐标;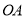 的长;
的长;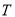 (
(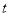 ,0)是
,0)是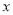 轴正半轴上的一个动点,当△ATO是等腰三角形时,求
轴正半轴上的一个动点,当△ATO是等腰三角形时,求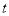 的值.
的值.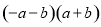 B.
B. 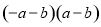
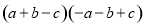 D.
D. 
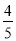 ,求BF的长.
,求BF的长.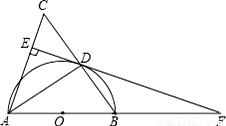
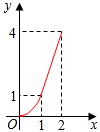
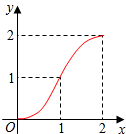
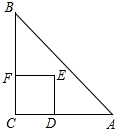 如图,Rt△ABC中,∠C=90°,AC=BC=2,正方形CDEF的顶点D、F分别在AB、BC边上,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象能表示y与x之间的函数关系的是( )
如图,Rt△ABC中,∠C=90°,AC=BC=2,正方形CDEF的顶点D、F分别在AB、BC边上,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象能表示y与x之间的函数关系的是( )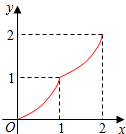

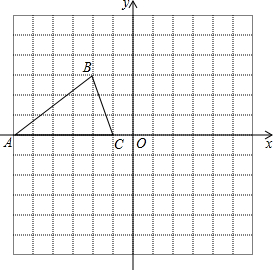 如图,已知△ABC的三个顶点坐标分别为A(-6,0)、B(-2,3)、C(-1,0).
如图,已知△ABC的三个顶点坐标分别为A(-6,0)、B(-2,3)、C(-1,0).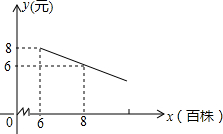 某花店计划用100个花盆培育一种花卉,用于国庆销售,已知花店从批发市场购进花苗的单价为y(元)和数量x(百株)之间的关系如图所示(其中x≥6),根据以往经验,每年的花卉供不应求,但若每个花盆培育6株,每株的销售单价为26元,每个花盆每增加1株,每株的销售单价就减少2元.
某花店计划用100个花盆培育一种花卉,用于国庆销售,已知花店从批发市场购进花苗的单价为y(元)和数量x(百株)之间的关系如图所示(其中x≥6),根据以往经验,每年的花卉供不应求,但若每个花盆培育6株,每株的销售单价为26元,每个花盆每增加1株,每株的销售单价就减少2元.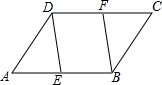 在?ABCD中,点E、F分别在AB、CD上,∠DEA=∠BFC,求证:四边形DEBF为平行四边形.
在?ABCD中,点E、F分别在AB、CD上,∠DEA=∠BFC,求证:四边形DEBF为平行四边形.