题目内容
11.计算或化简:(1)$\sqrt{3{a}^{2}}$÷3$\sqrt{\frac{a}{2}}$×$\frac{1}{2}$$\sqrt{\frac{2a}{3}}$
(2)$\sqrt{18}$-$\sqrt{\frac{9}{2}}$-$\frac{\sqrt{3}+\sqrt{6}}{\sqrt{3}}$+($\sqrt{3}$-2)0+$\sqrt{(1-\sqrt{2})^{2}}$
(3)$\frac{2{b}^{2}}{a+b}$-a+b
(4)1-$\frac{a-2}{a+1}$÷$\frac{{a}^{2}-4}{{a}^{2}+a}$.
分析 (1)按照二次根式的乘除计算方法计算即可;
(2)先化简,再进一步合并即可;
(3)通分计算;
(4)先算除法,再算减法.
解答 解:(1)原式=$\frac{1}{3}$$\sqrt{6a}$×$\frac{1}{2}$$\sqrt{\frac{2a}{3}}$
=$\frac{1}{3}$a;
(2)原式=3$\sqrt{2}$-$\frac{3}{2}$$\sqrt{2}$-1-$\sqrt{2}$+1+$\sqrt{2}$-1
=$\frac{3}{2}$$\sqrt{2}$-1;
(3)原式=$\frac{2{b}^{2}-{a}^{2}+{b}^{2}}{a+b}$
=$\frac{3{b}^{2}-{a}^{2}}{a+b}$;
(4)原式=1-$\frac{a-2}{a+1}$•$\frac{a(a+1)}{(a+2)(a-2)}$
=1-$\frac{a}{a+2}$
=$\frac{2}{a+2}$.
点评 本题考查的是二次根式的混合运算、分式的加减,在进行此类运算时,一般先把二次根式化为最简二次根式的形式,分是要通分、因式分解后再运算.

练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 △ABC中,AB=AC,AF⊥BC于点F,AD平分∠CAF,∠ADC=30°,BC=8,S△BCD=18,求BD的长.
△ABC中,AB=AC,AF⊥BC于点F,AD平分∠CAF,∠ADC=30°,BC=8,S△BCD=18,求BD的长.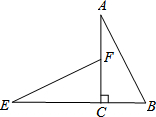 如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC.若AB=$\sqrt{5}$,BC=1,则线段BE的长为3,顶点A所运动过的路程等于π(保留π).
如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC.若AB=$\sqrt{5}$,BC=1,则线段BE的长为3,顶点A所运动过的路程等于π(保留π).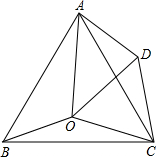 如图,点O是等边△ABC内一点,以CO为边作等边△COD,∠AOB=110°,∠BOC=α.
如图,点O是等边△ABC内一点,以CO为边作等边△COD,∠AOB=110°,∠BOC=α.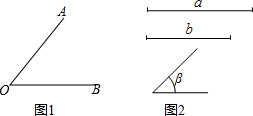 尺规作图(请保留作图痕迹,不写作法).
尺规作图(请保留作图痕迹,不写作法).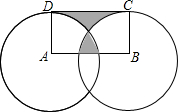 如图,分别以矩形ABCD的顶点A和B为圆心,作半径为1的两个圆正好分别经过C、D两点,若图中两块阴影部分的面积相等,则AB的长度是$\frac{π}{2}$.
如图,分别以矩形ABCD的顶点A和B为圆心,作半径为1的两个圆正好分别经过C、D两点,若图中两块阴影部分的面积相等,则AB的长度是$\frac{π}{2}$.