题目内容
19.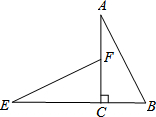 如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC.若AB=$\sqrt{5}$,BC=1,则线段BE的长为3,顶点A所运动过的路程等于π(保留π).
如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC.若AB=$\sqrt{5}$,BC=1,则线段BE的长为3,顶点A所运动过的路程等于π(保留π).
分析 先利用勾股定理计算出AC=2,再根据旋转的性质得CE=CA=2,∠ECF=∠ACB=90°,于是可判断点E在BC的延长线上,所以BE=BC+CE=3;由于点A运动的路径为以点A为圆心,CA为半径,圆心角为90°的弧,所以可根据弧长公式计算顶点A所运动过的路程长.
解答 解:在Rt△ABC中,∵AB=$\sqrt{5}$,BC=1,
∴AC=$\sqrt{(\sqrt{5})^{2}-{1}^{2}}$=2,
∵Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC,
∴CE=CA=2,∠ECF=∠ACB=90°,
∴点E在BC的延长线上,
∴BE=BC+CE=1+2=3;
顶点A所运动过的路程长=$\frac{90•π•2}{180}$=π.
故答案为3,π.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了勾股定理和弧长公式.

练习册系列答案
相关题目
14.对于图形的旋转,下列说法不正确的是( )
| A. | 对应点到旋转中心的距离相等 | B. | 图形上每一部分旋转的角度相同 | ||
| C. | 旋转前后的两个图形全等 | D. | 图形上每一点所经过的路程相同 |
9.下列计算正确的是( )
| A. | 2a5+a5=3a10 | B. | a2•a3=a6 | C. | (a2)3=a5 | D. | a10÷a2=a8 |
 已知直线y=$\frac{3}{4}$x+3分别交x轴、y轴于点A、B.
已知直线y=$\frac{3}{4}$x+3分别交x轴、y轴于点A、B. 已知实数a,b在数轴上的对应点如图所示,化简:$\sqrt{(a-b)^{2}}$-$\sqrt{{a}^{2}}$.
已知实数a,b在数轴上的对应点如图所示,化简:$\sqrt{(a-b)^{2}}$-$\sqrt{{a}^{2}}$.