题目内容
20.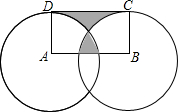 如图,分别以矩形ABCD的顶点A和B为圆心,作半径为1的两个圆正好分别经过C、D两点,若图中两块阴影部分的面积相等,则AB的长度是$\frac{π}{2}$.
如图,分别以矩形ABCD的顶点A和B为圆心,作半径为1的两个圆正好分别经过C、D两点,若图中两块阴影部分的面积相等,则AB的长度是$\frac{π}{2}$.
分析 设一块阴影部分的面积是M,再由扇形的面积公式及矩形的面积公式求解即可.
解答  解:设一块阴影部分的面积是M,
解:设一块阴影部分的面积是M,
∵两个圆的半径为1,
∴S扇形DAF=S扇形EBC=$\frac{1}{4}$π,
∴S扇形DAF+S扇形EBC=-M=S矩形ABC-M,即$\frac{π}{2}$-M=AB-M,解得AB=$\frac{π}{2}$.
故答案为:$\frac{π}{2}$.
点评 本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.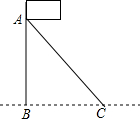 如图,AC是旗杆AB的一根拉线,测得BC=6米,∠ACB=50°,则拉线AC的长为( )
如图,AC是旗杆AB的一根拉线,测得BC=6米,∠ACB=50°,则拉线AC的长为( )
 如图,AC是旗杆AB的一根拉线,测得BC=6米,∠ACB=50°,则拉线AC的长为( )
如图,AC是旗杆AB的一根拉线,测得BC=6米,∠ACB=50°,则拉线AC的长为( )| A. | 6sin50° | B. | 6cos50° | C. | $\frac{6}{sin50°}$ | D. | $\frac{6}{cos50°}$ |
9.下列计算正确的是( )
| A. | 2a5+a5=3a10 | B. | a2•a3=a6 | C. | (a2)3=a5 | D. | a10÷a2=a8 |
 已知直线y=$\frac{3}{4}$x+3分别交x轴、y轴于点A、B.
已知直线y=$\frac{3}{4}$x+3分别交x轴、y轴于点A、B. 已知实数a,b在数轴上的对应点如图所示,化简:$\sqrt{(a-b)^{2}}$-$\sqrt{{a}^{2}}$.
已知实数a,b在数轴上的对应点如图所示,化简:$\sqrt{(a-b)^{2}}$-$\sqrt{{a}^{2}}$.