题目内容
8.我市校计划购买甲、乙两种树苗共200株来绿化校园,甲种树苗每株25元,乙种树苗每株30元,通过调查了解,甲乙两种树苗成活率分别是90%和95%.(1)若购买这种树苗共用去5600元,则甲、乙两种树苗各购买了多少株?
(2)如果要求这200株树苗的成活率不低于93%,那么乙种树苗至少要购买多少株.
分析 (1)设购买甲种树苗x棵,乙种树苗y棵,结合两种树苗共买了200株和购买钱数=单价×数量,列出关于x、y的二元一次方程组,解方程组即可得出结论;
(2)设购买乙种树苗a株,则购买甲种树苗200-a株,根据成活率=成活的棵数÷总棵数列出关于a的一元一次不等式,解不等式即可得出结论.
解答 解:(1)设购买甲种树苗x棵,乙种树苗y棵,
由已知得:$\left\{\begin{array}{l}{x+y=200}\\{25x+30y=5600}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=80}\\{y=120}\end{array}\right.$.
答:甲种树苗购买了80株,乙种树苗购买了120株.
(2)设购买乙种树苗a株,则购买甲种树苗200-a株,
由已知可得:$\frac{90%(200-a)+95%a}{200}$×100%≥93%,
解得:a≥120.
答:如果要求这200株树苗的成活率不低于93%,那么乙种树苗至少要购买120株.
点评 本题考查了二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:(1)列出关于x、y的二元一次方程组;(2)根据成活率列出关于a的一元一次不等式.本题属于基础题,难度不大,解决该题型题目时,根据各数量间的关系列出方程(方程组)是解题的关键.

练习册系列答案
相关题目
18. 如图,在△ABC中,∠ACB=90°,D为AB的中点,E为AC上一点,连接DE,并过点D作FD⊥ED,垂足为D,交BC于点F.若AC=BC=14,AE:EC=4:3,则tan∠EFC的值为( )
如图,在△ABC中,∠ACB=90°,D为AB的中点,E为AC上一点,连接DE,并过点D作FD⊥ED,垂足为D,交BC于点F.若AC=BC=14,AE:EC=4:3,则tan∠EFC的值为( )
 如图,在△ABC中,∠ACB=90°,D为AB的中点,E为AC上一点,连接DE,并过点D作FD⊥ED,垂足为D,交BC于点F.若AC=BC=14,AE:EC=4:3,则tan∠EFC的值为( )
如图,在△ABC中,∠ACB=90°,D为AB的中点,E为AC上一点,连接DE,并过点D作FD⊥ED,垂足为D,交BC于点F.若AC=BC=14,AE:EC=4:3,则tan∠EFC的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
3.以下列各组数作为三角形的三边长,其中不能构成直角三角形的是( )
| A. | 1,1,$\sqrt{2}$ | B. | 12,16,20 | C. | 1,$\frac{4}{3}$,$\frac{5}{3}$ | D. | 1,2,2 |
13.已知关于x的方程x2-3mx+5m-2=0的一个根为x=2,且这个方程的两个根恰好是等腰△ABC的两条边长,则△ABC的周长为( )
| A. | 8 | B. | 10 | C. | 8或10 | D. | 6或10 |
 如图是一块长、宽、高分别是6cm、4cm和3cm的长方体木块,一只蚂蚁要从顶点A出发,沿长方体的表面爬到和A相对的顶点B处吃食物,那么它需要爬行的最短路线的长是$\sqrt{85}$.
如图是一块长、宽、高分别是6cm、4cm和3cm的长方体木块,一只蚂蚁要从顶点A出发,沿长方体的表面爬到和A相对的顶点B处吃食物,那么它需要爬行的最短路线的长是$\sqrt{85}$.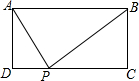 如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP相似时,DP=1或4或2.5.
如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP相似时,DP=1或4或2.5.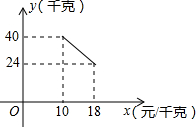 某经销商销售一种产品,这种产品的成本价为10元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克,且10≤x≤18)之间的函数关系如图所示,该经销商想要每天获得150元的销售利润,销售价应定为多少?列出关于x方程是(x-10)(-2x+60)=150(不需化简和解方程).
某经销商销售一种产品,这种产品的成本价为10元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克,且10≤x≤18)之间的函数关系如图所示,该经销商想要每天获得150元的销售利润,销售价应定为多少?列出关于x方程是(x-10)(-2x+60)=150(不需化简和解方程). 如图是由4个大小相同的正方体组合而成的几何体,其俯视图是( )
如图是由4个大小相同的正方体组合而成的几何体,其俯视图是( )


