题目内容
20.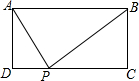 如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP相似时,DP=1或4或2.5.
如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP相似时,DP=1或4或2.5.
分析 需要分类讨论:△APD∽△PBC和△PAD∽△PBC,根据该相似三角形的对应边成比例求得DP的长度.
解答 解:①当△APD∽△PBC时,$\frac{AD}{PC}$=$\frac{PD}{BC}$,
即$\frac{2}{5-PD}$=$\frac{PD}{2}$,
解得:PD=1,或PD=4;
②当△PAD∽△PBC时,$\frac{AD}{BC}$=$\frac{PD}{PC}$,即$\frac{2}{2}$=$\frac{PD}{5-PD}$,
解得:DP=2.5.
综上所述,DP的长度是1或4或2.5.
故答案是:1或4或2.5.
点评 本题考查了矩形的性质,相似三角形的判定与性质.对于动点问题,需要分类讨论,以防漏解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.为了加强公民的节水意识,合理利用水资源,各地采用价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过6立方米时,水费按每立方米a元收费,超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按c元收费,该市某户今年9、10月份的用水量和所交水费如下表所示:
(1)求a,c的值(列方程组求解);
(2)设某户每月用水量x(立方米),应交水费y(元);分别写出当0≤x≤6,x≥6时,y关于x的函数关系;
(3)若该户11月份用水量为8立方米,求该户11月份水费是多少元?
| 月份 | 用水量(m3) | 收费(元) |
| 9 | 5 | 7.5 |
| 10 | 9 | 27 |
(2)设某户每月用水量x(立方米),应交水费y(元);分别写出当0≤x≤6,x≥6时,y关于x的函数关系;
(3)若该户11月份用水量为8立方米,求该户11月份水费是多少元?
5. 如图所示,将一个透明的圆柱形玻璃容器(不计壁厚)中装入体积为容器一半容积的水,当水平放置该容器时,水面的形状为( )
如图所示,将一个透明的圆柱形玻璃容器(不计壁厚)中装入体积为容器一半容积的水,当水平放置该容器时,水面的形状为( )
 如图所示,将一个透明的圆柱形玻璃容器(不计壁厚)中装入体积为容器一半容积的水,当水平放置该容器时,水面的形状为( )
如图所示,将一个透明的圆柱形玻璃容器(不计壁厚)中装入体积为容器一半容积的水,当水平放置该容器时,水面的形状为( )| A. | 圆 | B. | 椭圆 | ||
| C. | 一般的平行四边形 | D. | 矩形 |
 如图,AB∥CD,∠D=75°,∠CAD:∠BAC=2:1,则∠CAD=70.
如图,AB∥CD,∠D=75°,∠CAD:∠BAC=2:1,则∠CAD=70.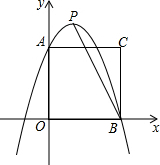 如图所示,将一边长为3的正方形放置到平面直角坐标系中,其顶点A、B均落在坐标轴上,一抛物线过点A、B,且顶点为P(1,4)
如图所示,将一边长为3的正方形放置到平面直角坐标系中,其顶点A、B均落在坐标轴上,一抛物线过点A、B,且顶点为P(1,4) 如图是一个转盘,转一次指针指向灰色部分的概率是$\frac{1}{3}$.
如图是一个转盘,转一次指针指向灰色部分的概率是$\frac{1}{3}$.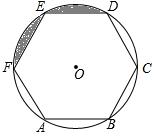 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1.
如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1.