题目内容
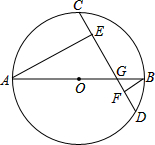 如图,已知⊙O的直径AB与弦CD相交于G,AE⊥CD于E,BF⊥CD于F,且⊙O的半径为10cm,CD=16cm,求AE-BF的长.
如图,已知⊙O的直径AB与弦CD相交于G,AE⊥CD于E,BF⊥CD于F,且⊙O的半径为10cm,CD=16cm,求AE-BF的长.考点:垂径定理,勾股定理,三角形中位线定理
专题:
分析:如图,作辅助线,综合运用垂径定理、勾股定理、三角形的中位线定理等几何知识点来分析、判断即可解决问题.
解答: 解:如图,连接OC,延长AE交⊙O于点H,连接BH;
解:如图,连接OC,延长AE交⊙O于点H,连接BH;
过点O作ON⊥BH于点N,交CD于点M;
则HN=BN,CM=DM=
CD=8,;
∵AB为⊙O的直径,
∴∠AHB=90°;
∵AE⊥CD,
∴CD∥BH;
∵ON⊥BH,BF⊥CD,
∴EH=MN=BF(设为x);
∵AO=B0,HN=BN,
∴ON为△ABH的中位线,
∴AH=2ON,
即AE+x=2(OM+x),AE-x=2OM;
由勾股定理得:
OM2=OC2-CG2=100-64=36,
∴OM=6,2OM=12;
∴AE-BF=12.
 解:如图,连接OC,延长AE交⊙O于点H,连接BH;
解:如图,连接OC,延长AE交⊙O于点H,连接BH;过点O作ON⊥BH于点N,交CD于点M;
则HN=BN,CM=DM=
| 1 |
| 2 |
∵AB为⊙O的直径,
∴∠AHB=90°;
∵AE⊥CD,
∴CD∥BH;
∵ON⊥BH,BF⊥CD,
∴EH=MN=BF(设为x);
∵AO=B0,HN=BN,
∴ON为△ABH的中位线,
∴AH=2ON,
即AE+x=2(OM+x),AE-x=2OM;
由勾股定理得:
OM2=OC2-CG2=100-64=36,
∴OM=6,2OM=12;
∴AE-BF=12.
点评:该命题以圆为载体,以垂径定理、勾股定理、三角形的中位线定理等几何知识点为考查的核心构造而成;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
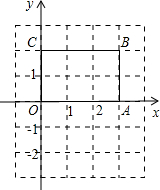 如图,在长方形OABC中,O为平面直角坐标系的原点,A,C的坐标分别为(3,0)、C(0,2),点B在第一象限.
如图,在长方形OABC中,O为平面直角坐标系的原点,A,C的坐标分别为(3,0)、C(0,2),点B在第一象限.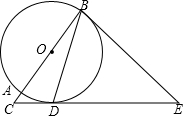 如图,AB为⊙O的直径,C为BA的延长线上一点,D为⊙O上一点,且∠CDA=∠CBD.
如图,AB为⊙O的直径,C为BA的延长线上一点,D为⊙O上一点,且∠CDA=∠CBD.