题目内容
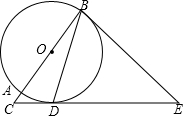 如图,AB为⊙O的直径,C为BA的延长线上一点,D为⊙O上一点,且∠CDA=∠CBD.
如图,AB为⊙O的直径,C为BA的延长线上一点,D为⊙O上一点,且∠CDA=∠CBD.(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,若tan∠ADC=
| 1 |
| 2 |
考点:切线的判定
专题:
分析:(1)如图,连接OD,证明∠CDO=90°问题即可解决;
(2)如图,作辅助线,首先证明△ADB∽△DMB,进而得到
=
;运用勾股定理结合正切的定义即可解决问题.
(2)如图,作辅助线,首先证明△ADB∽△DMB,进而得到
| AD |
| DB |
| DM |
| BM |
解答: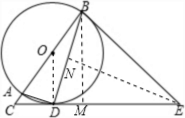 解:(1)如图,连接OD;
解:(1)如图,连接OD;
∵OA=OD,OB=OD;
∴∠OAD=∠ODA,∠OBD=∠ODB;
∵AB为⊙O的直径,
∴∠OAD+∠OBD=90°,
∴∠ODA+∠OBD=90°,
而∠CDA=∠CBD,
∴∠ODA+∠CDA=90°,
即∠CDO=90°,
∴CD是⊙O的切线.
(2)如图,过点B、E分别作BM⊥DE,MN⊥BD,垂足为M、N.
∵CD为⊙O的切线,
∴∠ADM=∠BAD,而∠ADB=∠DMB,
∴△ADB∽△DMB,
∴
=
;
∵tan∠ADC=tan∠ABD=
=
,
∴
=
;
设DM=x,则BM=2x;
∵BE、DE是⊙O的切线,
∴BE=DE(设为y),
则ME=y-x;由勾股定理得:
y2=(y-x)2+(2x)2,
解得:y=
,ME=
-x=
,
∴tan∠E=
=
,
即sin∠E的值为
.
 解:(1)如图,连接OD;
解:(1)如图,连接OD;∵OA=OD,OB=OD;
∴∠OAD=∠ODA,∠OBD=∠ODB;
∵AB为⊙O的直径,
∴∠OAD+∠OBD=90°,
∴∠ODA+∠OBD=90°,
而∠CDA=∠CBD,
∴∠ODA+∠CDA=90°,
即∠CDO=90°,
∴CD是⊙O的切线.
(2)如图,过点B、E分别作BM⊥DE,MN⊥BD,垂足为M、N.
∵CD为⊙O的切线,
∴∠ADM=∠BAD,而∠ADB=∠DMB,
∴△ADB∽△DMB,
∴
| AD |
| DB |
| DM |
| BM |
∵tan∠ADC=tan∠ABD=
| AD |
| BD |
| 1 |
| 2 |
∴
| DM |
| BM |
| 1 |
| 2 |
设DM=x,则BM=2x;
∵BE、DE是⊙O的切线,
∴BE=DE(设为y),
则ME=y-x;由勾股定理得:
y2=(y-x)2+(2x)2,
解得:y=
| 5x |
| 2 |
| 5x |
| 2 |
| 3x |
| 2 |
∴tan∠E=
| 2x | ||
|
| 4 |
| 3 |
即sin∠E的值为
| 4 |
| 3 |
点评:考查了切线的判定,该命题以圆为载体,以切线的判定、圆周角定理及其推论、相似三角形的判定及其应用为核心构造而成;解题的关键是灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
相关题目
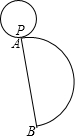 如图是一个圆锥的表面展开图,其中小圆是圆锥的底面,点A,B是半圆直径的两个端点,开始时小圆上的点P与A重合,当这个小圆紧贴半圆滚动1周后,你会发现什么现象?由此,你发现半圆的直径与小圆的半径有什么关系.
如图是一个圆锥的表面展开图,其中小圆是圆锥的底面,点A,B是半圆直径的两个端点,开始时小圆上的点P与A重合,当这个小圆紧贴半圆滚动1周后,你会发现什么现象?由此,你发现半圆的直径与小圆的半径有什么关系.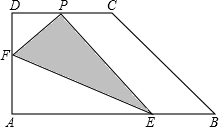 如图,直角梯形纸片ABCD,AD⊥AB,AB=8,AD=CD=4,点E、F分别在线段AB、AD上,将△AEF沿EF翻折,点A的落点记为P.当P落在直角梯形ABCD内部时,PD的最小值等于
如图,直角梯形纸片ABCD,AD⊥AB,AB=8,AD=CD=4,点E、F分别在线段AB、AD上,将△AEF沿EF翻折,点A的落点记为P.当P落在直角梯形ABCD内部时,PD的最小值等于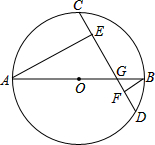 如图,已知⊙O的直径AB与弦CD相交于G,AE⊥CD于E,BF⊥CD于F,且⊙O的半径为10cm,CD=16cm,求AE-BF的长.
如图,已知⊙O的直径AB与弦CD相交于G,AE⊥CD于E,BF⊥CD于F,且⊙O的半径为10cm,CD=16cm,求AE-BF的长.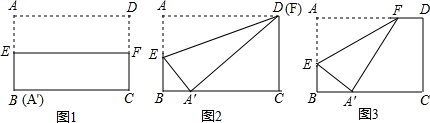
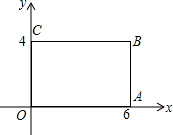 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的
如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的