题目内容
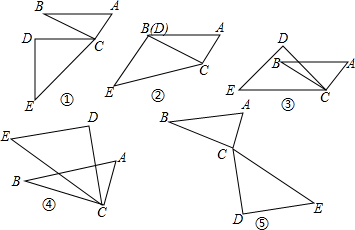
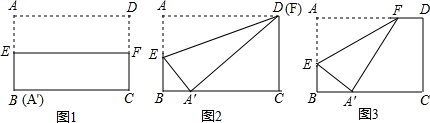
如图所示,在一副三角板ABC和三角板DEC中,∠ACB=∠CDE=90°,∠BAC=60°,∠DEC=45°.
(1)当AB∥DC时,如图①,求∠DCB的度数;
(2)当CD与CB重合时,如图②,判断DE与AC的位置关系,并说明理由;
(3)如图③,当∠DCB等于多少度时,AB∥EC?
(4)当AB∥ED时,如图④⑤,分别求∠DCB的度数.
(1)当AB∥DC时,如图①,求∠DCB的度数;
(2)当CD与CB重合时,如图②,判断DE与AC的位置关系,并说明理由;
(3)如图③,当∠DCB等于多少度时,AB∥EC?
(4)当AB∥ED时,如图④⑤,分别求∠DCB的度数.

考点:平行线的判定与性质,垂线
专题:计算题
分析:(1)先根据互余计算出∠B=30°,然后根据平行线的性质即可得到∠BCD=∠B=30°;
(2)由于∠ACB=∠CDE=90°,根据平行线的判定易得DE∥AC;
(3)先利用互余计算出∠DCE=45°,根据平行线的判定方法,当∠ECB=∠B=30°时,AB∥CE,易得∠DCB=15°;
(4)如图④,根据平行线的性质由AB∥DE得到∠CFB=∠CDE=90°,再根据互余可计算出∠DCB的度数;
如图⑤,作CF∥AB,根据平行线的性质得CF∥DE,且∠BCF=∠B=30°,∠DCF=∠CDE=90°,则利用∠BCD=∠BCF+∠DCF进行计算.
(2)由于∠ACB=∠CDE=90°,根据平行线的判定易得DE∥AC;
(3)先利用互余计算出∠DCE=45°,根据平行线的判定方法,当∠ECB=∠B=30°时,AB∥CE,易得∠DCB=15°;
(4)如图④,根据平行线的性质由AB∥DE得到∠CFB=∠CDE=90°,再根据互余可计算出∠DCB的度数;
如图⑤,作CF∥AB,根据平行线的性质得CF∥DE,且∠BCF=∠B=30°,∠DCF=∠CDE=90°,则利用∠BCD=∠BCF+∠DCF进行计算.
解答:解:(1)∵∠ACB=90°,∠BAC=60°,
∴∠B=30°,
∵AB∥CD,
∴∠BCD=∠B=30°;
(2)当CD与CB重合时,DE与AC平行.理由如下:
∵∠ACB=∠CDE=90°,
∴DE∥AC;
(3)∵∠CDE=90°,∠DEC=45°,
 ∴∠DCE=45°,
∴∠DCE=45°,
当∠ECB=∠B=30°时,AB∥CE,
此时∠DCB=∠DEC-∠ECB=15°;
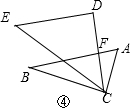
(4)如图④,∵AB∥DE,
∴∠CFB=∠CDE=90°,
 ∵∠B=30°,
∵∠B=30°,
∴∠DCB=90°-30°=60°;
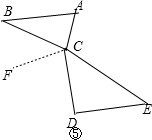
如图⑤,作CF∥AB,
∵AB∥DE,
∴CF∥DE,
∴∠BCF=∠B=30°,∠DCF=∠CDE=90°,
∴∠BCD=∠BCF+∠DCF=120°.
∴∠B=30°,
∵AB∥CD,
∴∠BCD=∠B=30°;
(2)当CD与CB重合时,DE与AC平行.理由如下:
∵∠ACB=∠CDE=90°,
∴DE∥AC;
(3)∵∠CDE=90°,∠DEC=45°,
 ∴∠DCE=45°,
∴∠DCE=45°,当∠ECB=∠B=30°时,AB∥CE,
此时∠DCB=∠DEC-∠ECB=15°;
(4)如图④,∵AB∥DE,
∴∠CFB=∠CDE=90°,
 ∵∠B=30°,
∵∠B=30°,∴∠DCB=90°-30°=60°;
如图⑤,作CF∥AB,
∵AB∥DE,
∴CF∥DE,
∴∠BCF=∠B=30°,∠DCF=∠CDE=90°,
∴∠BCD=∠BCF+∠DCF=120°.
点评:本题考查了平行线的判定与性质:平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.应用平行线的判定和性质定理时,一定要弄清题设和结论,切莫混淆.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列各数:
,0,4.2121121112,
,2.369,-5;其中无理数的个数有( )
| π |
| 3 |
| 23 |
| 7 |
| A、4个 | B、3个 | C、2个 | D、1个 |
下列说法正确的是( )
| A、符号不同的两个数互为相反数 |
| B、倒数等于本身的数是0,1,-1 |
| C、平方等于9的数是3 |
| D、负数的偶次幂是正数 |
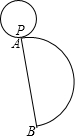 如图是一个圆锥的表面展开图,其中小圆是圆锥的底面,点A,B是半圆直径的两个端点,开始时小圆上的点P与A重合,当这个小圆紧贴半圆滚动1周后,你会发现什么现象?由此,你发现半圆的直径与小圆的半径有什么关系.
如图是一个圆锥的表面展开图,其中小圆是圆锥的底面,点A,B是半圆直径的两个端点,开始时小圆上的点P与A重合,当这个小圆紧贴半圆滚动1周后,你会发现什么现象?由此,你发现半圆的直径与小圆的半径有什么关系.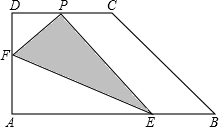 如图,直角梯形纸片ABCD,AD⊥AB,AB=8,AD=CD=4,点E、F分别在线段AB、AD上,将△AEF沿EF翻折,点A的落点记为P.当P落在直角梯形ABCD内部时,PD的最小值等于
如图,直角梯形纸片ABCD,AD⊥AB,AB=8,AD=CD=4,点E、F分别在线段AB、AD上,将△AEF沿EF翻折,点A的落点记为P.当P落在直角梯形ABCD内部时,PD的最小值等于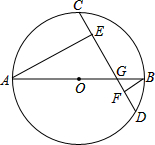 如图,已知⊙O的直径AB与弦CD相交于G,AE⊥CD于E,BF⊥CD于F,且⊙O的半径为10cm,CD=16cm,求AE-BF的长.
如图,已知⊙O的直径AB与弦CD相交于G,AE⊥CD于E,BF⊥CD于F,且⊙O的半径为10cm,CD=16cm,求AE-BF的长.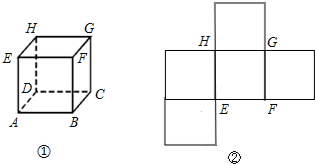
 如图,在8×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为
如图,在8×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为