题目内容
某学习小组8名同学参加英语测试(满分20分)的平均成绩是15分,其中5名男生成绩的方差是8,三名女生的成绩分别是13分,15分,17分.求这个学习小组8名同学考试成绩的方差.
考点:方差
专题:
分析:根据平均数的计算公式先求出这5名男生的平均成绩,再根据方差公式进行计算,即可得出答案.
解答:解:5名男生的平均成绩是
=15(分),
设三名男生的成绩为x1,x2,x3,x4,x5,则:
S2=
[(x1-
)2+(x2-
)2+(x3-
)2+(x4-
)2+(x5-
)2]=40,
则这个学习小组8名同学考试成绩的方差是:
[(x1-
)2+(x2-
)2+(x3-
)2+(x4-
)2+(x5-
)2+(13-15)2+(15-15)2+(17-15)2]
=
(40+4+4)
=5.5(分).
答:这个学习小组8名同学考试成绩的方差是5.5分.
| 15×8-13-15-17 |
| 5 |
设三名男生的成绩为x1,x2,x3,x4,x5,则:
S2=
| 1 |
| 5 |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
则这个学习小组8名同学考试成绩的方差是:
| 1 |
| 8 |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
=
| 1 |
| 8 |
=5.5(分).
答:这个学习小组8名同学考试成绩的方差是5.5分.
点评:本题考查了平均数和方差,一般地设n个数据,x1,x2,…xn的平均数为
,则方差S2=
[(x1-
)2+(x2-
)2+…+(xn-
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
. |
| x |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |

练习册系列答案
相关题目
下列各式,分解因式正确的是( )
| A、a2-b2=(a-b)2 | ||
| B、a2-2ab+b2=(a-b)2 | ||
C、x2+x3=x3(
| ||
| D、xy+xz+x=x(y+z) |
在下面图形中,不能折成正方体的是( )
A、 |
B、 |
C、 |
D、 |
把一个正方体展开,不可能得到的是( )
A、 |
B、 |
C、 |
D、 |
 如图,在Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,求线段BN的长.
如图,在Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,求线段BN的长.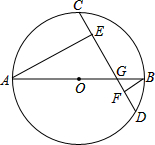 如图,已知⊙O的直径AB与弦CD相交于G,AE⊥CD于E,BF⊥CD于F,且⊙O的半径为10cm,CD=16cm,求AE-BF的长.
如图,已知⊙O的直径AB与弦CD相交于G,AE⊥CD于E,BF⊥CD于F,且⊙O的半径为10cm,CD=16cm,求AE-BF的长.