��Ŀ����
8�������Ķ�������ϲ������������⣺��һ�κ���y=kx+b��k��0���У����������±��Σ�kx=y-b$x=\frac{1}{k}y-\frac{b}{k}$��k��0��
�ٰ�$x=\frac{1}{k}y-\frac{b}{k}$�е�x��y�������õ�$y=\frac{1}{k}x-\frac{b}{k}$��
��ʱ���ǾͰѺ���$y=\frac{1}{k}x-\frac{1}{k}b$��k��0����������y=kx+b�ķ�������
ͬʱ�����������������ʽ��ͬ���Ա�����ȡֵ��ΧҲ��ͬ���������������Ϊͬһ������
��1������$y=\frac{1}{2}x+1$�����ķ������Ľ������ꣻ
��2��������y=kx+2�����ķ�������ͬһ��������k��ֵ��
���� ��1���ó���������Ȼ���������̣��ⷽ���鼴����ã�
��2���ó�������������ͬһ�����ĸ���ó�k=$\frac{1}{k}$��2=-$\frac{2}{k}$���������k=-1��
��� �⣺��1���ɺ���$y=\frac{1}{2}x+1$��֪���ķ�����Ϊy=2x-2��
��$\left\{\begin{array}{l}{y=\frac{1}{2}x+1}\\{y=2x-2}\end{array}\right.$��$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$��
�ຯ��$y=\frac{1}{2}x+1$�����ķ������Ľ�������Ϊ��2��2����
��2���ɺ���y=kx+2��֪���ķ�������y=$\frac{1}{k}$x-$\frac{2}{k}$��
�ߺ���y=kx+2�����ķ�������ͬһ������
��k=$\frac{1}{k}$��2=-$\frac{2}{k}$��
��k=-1��
���� ���⿼��������ֱ�ߵĽ������⣬�ó��������Ľ���ʽ�ǽ���Ĺؼ���

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 ��ͼ��ʾ����֪��ABC=��ADC=90�㣬E��AC��һ�㣬AB=AD��
��ͼ��ʾ����֪��ABC=��ADC=90�㣬E��AC��һ�㣬AB=AD�� С��ij������9ʱ�����г��뿪�ң�17ʱ�ؼң��������������ҵľ�����ʱ��ı仯�������ͼ��ʾ��
С��ij������9ʱ�����г��뿪�ң�17ʱ�ؼң��������������ҵľ�����ʱ��ı仯�������ͼ��ʾ�� ��ͼ���ڱ߳�Ϊa��������ABCD�У�M��CD���е㣬N��BC��һ�㣬��BN=$\frac{3}{4}$BC�����AMN�������
��ͼ���ڱ߳�Ϊa��������ABCD�У�M��CD���е㣬N��BC��һ�㣬��BN=$\frac{3}{4}$BC�����AMN������� ��ͼ��C��D���߶�AB�ֳ�2��3��4�����֣�E��F�ֱ���AC��BD���е㣬��AB=36����EF�ij���
��ͼ��C��D���߶�AB�ֳ�2��3��4�����֣�E��F�ֱ���AC��BD���е㣬��AB=36����EF�ij���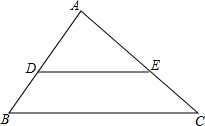 ��ͼ���ڡ�ABC�У���D��E�ֱ���AB��AC�ϵĵ㣬DE��BC��AD=2BD��S��ABC=36�����ı���BCED�����Ϊ20��
��ͼ���ڡ�ABC�У���D��E�ֱ���AB��AC�ϵĵ㣬DE��BC��AD=2BD��S��ABC=36�����ı���BCED�����Ϊ20��