题目内容
2．
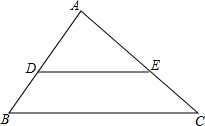如图，在△ABC中，点D、E分别是AB和AC上的点，DE∥BC，AD=2BD，S△ABC=36，则四边形BCED的面积为20．
分析 先求出$\frac{AD}{AB}$，再求出△ADE和△ABC相似，然后根据相似三角形面积的比等于相似比的平方求出△ADE的面积，再求解即可．
解答 解：∵AD=2BD，
∴$\frac{AD}{BD}$=2，
∴$\frac{AD}{AB}$=$\frac{2}{3}$，
∵DE∥BC，
∴△ADE∽△ABC，
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{4}{9}$，
∵S△ABC=36，
∴△ADE的面积=36×$\frac{4}{9}$=16．
∴四边形BCED的面积=36-16=20
故答案为：20．
点评 本题考查了相似三角形的判定与性质，熟悉相似三角形的性质：相似三角形的面积比是相似比的平方．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
9．
已知三角形A₁B₁C₁是由三角形ABC经过平移得到的，它们各对应顶点在平面直角坐标系中的坐标如下表所示：
（1）观察表中各对应点坐标的变化，并填空：a=0，b=2，c=9；
（2）在平面直角坐标系中画出三角形ABC及三角形A₁B₁C₁．
已知三角形A₁B₁C₁是由三角形ABC经过平移得到的，它们各对应顶点在平面直角坐标系中的坐标如下表所示：| 三角形ABC | A（a，0 ） | B（3，0） | C（5，5） |
| 三角形A₁B₁C₁ | A₁（4，2） | B₁（7，b） | C₁（c，7） |
（2）在平面直角坐标系中画出三角形ABC及三角形A₁B₁C₁．
如图，在△ABC中，点D、E分别在边AB、BC上，且BD=6cm，DA=3cm，BE=4cm，若DE平行于AC，则EC=2cm．
14．已知a3=2，b5=3，则a、b的大小关系是（ ）
| A． | a＜b | B． | a＞b | C． | a=b | D． | 不确定 |
如图，在四边形ABCD中，∠B=∠D=90°，AE、CF分别平分∠BAD和∠BCD．