题目内容
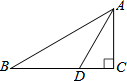 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,DC=
如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,DC=| 3 |
(1)求∠B的度数;
(2)求AB及BC的长.
考点:解直角三角形
专题:
分析:(1)根据三角函数值求得∠DAC=30°,从而求得∠BAC=2∠DAC=60°,即可求得∠B的度数;
(2)根据含有30°的直角三角形的性质即可求得AB的长,根据三角函数值即可求得BC的长.
(2)根据含有30°的直角三角形的性质即可求得AB的长,根据三角函数值即可求得BC的长.
解答:解:(1)∵在△ACD中,∠C=90°,CD=
,AC=3,
∴tan∠DAC=
=
,
∴∠DAC=30°,
∵AD平分∠BAC,
∴∠BAC=2∠DAC=60°,
∴∠B=30°.
(2)∵在Rt△ABC中,∠C=90°,∠B=30°,AC=3,
∴AB=2AC=6,
∴BC=
=
=3
.
| 3 |
∴tan∠DAC=
| CD |
| AC |
| ||
| 3 |
∴∠DAC=30°,
∵AD平分∠BAC,
∴∠BAC=2∠DAC=60°,
∴∠B=30°.
(2)∵在Rt△ABC中,∠C=90°,∠B=30°,AC=3,
∴AB=2AC=6,
∴BC=
| AC |
| tanB |
| 3 | ||||
|
| 3 |
点评:本题考查了直角三角形的性质以及解直角三角函数,熟练掌握特殊角的三角函数值是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
方程x2-2x+1=0的根是( )
| A、x1=1,x2=-1 | ||
B、x=-1±
| ||
| C、无实根 | ||
| D、x1=x2=1 |
在平面直角坐标系中,若⊙O是以原点为圆心,2为半径的圆,则点M(1,1)在( )
| A、⊙O内 | B、⊙O外 |
| C、⊙O上 | D、不能确定 |
已知两点A(-3,y1),B(5,y2)均在抛物线y=ax2+bx+c(a≠0)上,点C(x0,y0)是该抛物线的顶点,若y0≥y1>y2,则x0的取值范围是( )
| A、x0<5 |
| B、1<x0<5 |
| C、-3≤x0<1 |
| D、x0<1 |
 如图,在平面直角坐标系中,已知直线与x轴交于点A(-1,0),与y轴交于点C(0,-2).线段AC的中垂线交x轴于点B(
如图,在平面直角坐标系中,已知直线与x轴交于点A(-1,0),与y轴交于点C(0,-2).线段AC的中垂线交x轴于点B(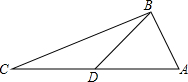 如图,在△ABC中,AB=5,BC=12,AC=13,点D是AC的中点,则BD=
如图,在△ABC中,AB=5,BC=12,AC=13,点D是AC的中点,则BD= 如图,过?ABCD的顶点C的直线交AB的延长线于点E,交AD的延长线于点F,若∠FCD=∠ECB,AF=8,则?ABCD的周长为
如图,过?ABCD的顶点C的直线交AB的延长线于点E,交AD的延长线于点F,若∠FCD=∠ECB,AF=8,则?ABCD的周长为