题目内容
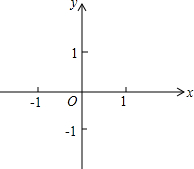 如图,在平面直角坐标系中,已知直线与x轴交于点A(-1,0),与y轴交于点C(0,-2).线段AC的中垂线交x轴于点B(
如图,在平面直角坐标系中,已知直线与x轴交于点A(-1,0),与y轴交于点C(0,-2).线段AC的中垂线交x轴于点B(| 3 |
| 2 |
(1)求直线AC的表达式.
(2)求出点D的坐标和△BAD的面积.
(3)过点B作y轴的平行线BH,借助△BAD的一边构造与△BAD面积相等的三角形,第三个点P在直线BH上,求出符合条件的点P的坐标.
考点:一次函数综合题
专题:
分析:(1)利用待定系数法可得出直线AC的表达式.
(2)由D点是线段AC的中点,可得出D的坐标,利用S△BAD=
AB•D纵坐标即可求出△BAD的面积.
(3)分两种情况:当以AB为一边时;当以BD为一边时;分别求解即可.
(2)由D点是线段AC的中点,可得出D的坐标,利用S△BAD=
| 1 |
| 2 |
(3)分两种情况:当以AB为一边时;当以BD为一边时;分别求解即可.
解答:解:(1)设直线AC的表达式为y=kx+b,
∵点A(-1,0),点C(0,-2).
∴把点A(-1,0),点C(0,-2)代入y=kx+b,得
,
解得
.
∴直线AC的表达式为y=-2x-2.
(2)如图1,

∵D点是线段AC的中点,
∴D(-
,-1),
S△BAD=
AB•D纵坐标=
×(1+
)×1=
.
(3)如图,

①当以AB为一边时,过点D作l′∥x轴,交BH于点P,则△ABP与△BAD面积相等的三角形,
∵点D(-
,-1),
∴P(
,-1)
点P关于点B的对称点P′(
,1)也满足△ABP与△BAD面积相等的三角形,
②当以BD为一边时,过点C作m∥BD轴,交BH于点P,则△ABP与△BAD面积相等的三角形,
∵D(-
,-1),B(
,0),
可得直线BD的解析式为y=
x-
,
设直线m的解析式为y=
x+b,
∵直线m过(0,-2),
∴直线m的解析式为y=
x-2,
∴直线m与BH的交点为P(
,-
),
点P关于点B的对称点P′(
,
)也满足△ABP与△BAD面积相等的三角形,
综上所述点P的坐标为:(
,-1),(
,1),(
,-
)或(
,
),
∵点A(-1,0),点C(0,-2).
∴把点A(-1,0),点C(0,-2)代入y=kx+b,得
|
解得
|
∴直线AC的表达式为y=-2x-2.
(2)如图1,

∵D点是线段AC的中点,
∴D(-
| 1 |
| 2 |
S△BAD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
(3)如图,

①当以AB为一边时,过点D作l′∥x轴,交BH于点P,则△ABP与△BAD面积相等的三角形,
∵点D(-
| 1 |
| 2 |
∴P(
| 3 |
| 2 |
点P关于点B的对称点P′(
| 3 |
| 2 |
②当以BD为一边时,过点C作m∥BD轴,交BH于点P,则△ABP与△BAD面积相等的三角形,
∵D(-
| 1 |
| 2 |
| 3 |
| 2 |
可得直线BD的解析式为y=
| 1 |
| 2 |
| 3 |
| 4 |
设直线m的解析式为y=
| 1 |
| 2 |
∵直线m过(0,-2),
∴直线m的解析式为y=
| 1 |
| 2 |
∴直线m与BH的交点为P(
| 3 |
| 2 |
| 5 |
| 4 |
点P关于点B的对称点P′(
| 3 |
| 2 |
| 5 |
| 4 |
综上所述点P的坐标为:(
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
| 3 |
| 2 |
| 5 |
| 4 |
点评:本题主要考查了一次函数的综合题,解题的关键是数形结合,利用分类讨论的思想.

练习册系列答案
相关题目
在Rt△ABC中,∠C=90°,AC=5,BC=12,则点C到AB的距离是( )
| A、13 | ||
| B、5 | ||
| C、6 | ||
D、
|
某种商品的进价为300元,出售标价为440元,后来由于该商品积压,商店准备打折销售,但要保证利润率为10%,则商店可打( )
| A、6折 | B、6.5折 |
| C、7.3折 | D、7.5折 |
 如图,已知点A的坐标分别为(0,0),B的坐标分别为(4,0),
如图,已知点A的坐标分别为(0,0),B的坐标分别为(4,0),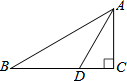 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,DC=
如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,DC= 如图,直线AB、CD、EF相交于点O,OG⊥CD,∠BOD=32°.
如图,直线AB、CD、EF相交于点O,OG⊥CD,∠BOD=32°.