题目内容
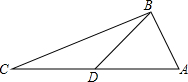 如图,在△ABC中,AB=5,BC=12,AC=13,点D是AC的中点,则BD=
如图,在△ABC中,AB=5,BC=12,AC=13,点D是AC的中点,则BD=考点:勾股定理的逆定理,直角三角形斜边上的中线
专题:
分析:由△ABC的三边长,利用勾股定理的逆定理判断出三角形为直角三角形,且AC为斜边,再由D为斜边上的中点,得到BD为斜边上的中线,利用直角三角形斜边上的中线等于斜边的一半,即可求出BD的长.
解答:解:∵AB=5,BC=12,AC=13,
∴AB2+BC2=25+144=169,AC2=132=169,即AB2+BC2=AC2,
∴△ABC为以AC为斜边的直角三角形,
又∵D为AC的中点,即BD为斜边上的中线,
∴BD=
AC=6.5.
故答案为:6.5.
∴AB2+BC2=25+144=169,AC2=132=169,即AB2+BC2=AC2,
∴△ABC为以AC为斜边的直角三角形,
又∵D为AC的中点,即BD为斜边上的中线,
∴BD=
| 1 |
| 2 |
故答案为:6.5.
点评:此题考查了勾股定理的逆定理,以及直角三角形斜边上的中线性质,熟练掌握定理及性质是解本题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
下列说法中正确的是( )
| A、近似数3.10与近似数3.1的精确度一样 |
| B、近似数3.1×103与近似数3100的精确度一样 |
| C、近似数3.10与近似数0.310都有三个有效数字 |
| D、将3.145精确到百分位后,有四个有效数字 |
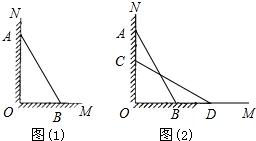 如图(1),一架长为20米云梯AB斜靠在竖直的墙ON上,这时云梯下端B到墙底端O的距离BO=12米,在下列结论中,正确的是( )
如图(1),一架长为20米云梯AB斜靠在竖直的墙ON上,这时云梯下端B到墙底端O的距离BO=12米,在下列结论中,正确的是( )A、当消防员爬到距离地面
| ||
| B、如图(2),当梯子顶端A沿墙下滑3米时,底端B向外移动3米 | ||
| C、如图(2),在梯子下滑过程中,梯子AB与墙ON,地面OM构成的三角形面积存在最大值,最大值为100米2 | ||
D、若在射线ON上存在一点G,使得△ABG为等腰三角形,则AG=
|
已知△ABC,求作一点P,使点P到∠A两边的距离相等,且PB=PC,下列确定点P的方法,正确的是( )
| A、P为∠A,∠B两角平分线的交点 |
| B、P为AC,AB两边的垂直平分线的交点 |
| C、P为AC,AB两边上的高的交点 |
| D、P为∠A的平分线与边BC的垂直平分线的交点 |
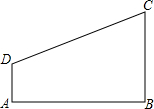 已知,如图,四边形ABCD,∠A=∠B=Rt∠
已知,如图,四边形ABCD,∠A=∠B=Rt∠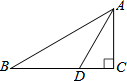 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,DC=
如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,DC=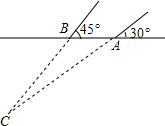 如图,在修建某条地铁时,科技人员利用探测仪在地面A、B两个探测点探测到地下C处有金属回声.已知A、B两点相距8米,探测线AC,BC与地面的夹角分别是30°和45°,试确定有金属回声的点C的深度是多少米?
如图,在修建某条地铁时,科技人员利用探测仪在地面A、B两个探测点探测到地下C处有金属回声.已知A、B两点相距8米,探测线AC,BC与地面的夹角分别是30°和45°,试确定有金属回声的点C的深度是多少米?