题目内容
已知两点A(-3,y1),B(5,y2)均在抛物线y=ax2+bx+c(a≠0)上,点C(x0,y0)是该抛物线的顶点,若y0≥y1>y2,则x0的取值范围是( )
| A、x0<5 |
| B、1<x0<5 |
| C、-3≤x0<1 |
| D、x0<1 |
考点:二次函数图象上点的坐标特征
专题:
分析:由于y1<y2≤y0,可判断抛物线开口向下,分类讨论:根据二次函数的性质得两点A(-3,y1),B(5,y2)都在对称轴右侧,此时x0≥-3;当两点A(-3,y1),B(5,y2)在对称轴两侧,则点(-3,y1)离对称轴要近,于是可判断x0<1,然后综合两种情况即可.
解答:解:∵点C(x0,y0)是该抛物线的顶点,y0≥y1>y2,
∴抛物线开口向下,
当两点A(-3,y1),B(5,y2)都在对称轴右侧,则x0≤-3;
当两点A(-3,y1),B(5,y2)在对称轴两侧,则点(-3,y1)离对称轴要近,所以-3≤x0<1,
∴x0<1.
故选D.
∴抛物线开口向下,
当两点A(-3,y1),B(5,y2)都在对称轴右侧,则x0≤-3;
当两点A(-3,y1),B(5,y2)在对称轴两侧,则点(-3,y1)离对称轴要近,所以-3≤x0<1,
∴x0<1.
故选D.
点评:本题考查了二次函数图象上点的坐标特征,主要利用了二次函数的增减性与对称性,根据顶点的纵坐标最大确定出抛物线开口方向是解题的关键.

练习册系列答案
相关题目
已知△ABC,求作一点P,使点P到∠A两边的距离相等,且PB=PC,下列确定点P的方法,正确的是( )
| A、P为∠A,∠B两角平分线的交点 |
| B、P为AC,AB两边的垂直平分线的交点 |
| C、P为AC,AB两边上的高的交点 |
| D、P为∠A的平分线与边BC的垂直平分线的交点 |
下列四个数中,结果为负数的是( )
A、-(-
| ||
B、|-
| ||
C、(-
| ||
D、-|-
|
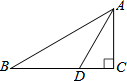 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,DC=
如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,DC=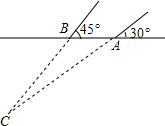 如图,在修建某条地铁时,科技人员利用探测仪在地面A、B两个探测点探测到地下C处有金属回声.已知A、B两点相距8米,探测线AC,BC与地面的夹角分别是30°和45°,试确定有金属回声的点C的深度是多少米?
如图,在修建某条地铁时,科技人员利用探测仪在地面A、B两个探测点探测到地下C处有金属回声.已知A、B两点相距8米,探测线AC,BC与地面的夹角分别是30°和45°,试确定有金属回声的点C的深度是多少米?



 如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=118°,则∠α=
如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=118°,则∠α=