题目内容
4.(1)解方程:①?x2-3x+2=0?
②$\frac{10}{{x}^{2}+x-6}$+$\frac{2}{2-x}$=1
(2)解不等式组:$\left\{\begin{array}{l}{2x-3≥x+1}\\{x-2>\frac{1}{2}(x+1)}\end{array}\right.$.
分析 (1)利用因式分解法解方程;
(2)先去方程把分式方程化为整式方程得到x2+3x-10=0,再利用因式分解法解整式方程,然后进行检验确定原方程的解;
(3)分别解两个不等式得到x≥4和x>5,然后利用同大取大确定不等式组的解集.
解答 解:(1)(x-1)(x-2)=0,
x-1=0或x-2=0,
所以x1=1,x2=2;
(2)原方程变形为$\frac{10}{(x+3)(x-2)}$-$\frac{2}{x-2}$=1,
去分母得10-2(x+3)=(x+3)(x-2),
整理得x2+3x-10=0,
解得x1=2,x2=-5,
检验:当x=2时,(x+3)(x-2)=0,所以x=2为原方程的增根;
当x=-5时,(x+3)(x-2)≠0,所以x=-5为原方程的根,
所以原方程的解为x=-5;
(3)$\left\{\begin{array}{l}{2x-3≥x+1①}\\{x-2>\frac{1}{2}(x+1)②}\end{array}\right.$,
解①得x≥4,
解②得x>5,
所以不等式组的解集为x>5.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了解分式方程和一元一次不等式组.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.下列方程组的解中是二元一次方程组$\left\{\begin{array}{l}{2x+y=2}\\{-x+y=5}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=6}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-3}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=4}\end{array}\right.$ |
9.多边形的边数增加1时、它的内角和与外角和( )
| A. | 都不变 | B. | 内角和增加180°外角和不变 | ||
| C. | 都增加180° | D. | 内角和增加180°外角和减少180° |
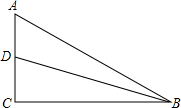 如图,Rt△ABC中,∠C=90°,BD是∠ABC的平分线,交AC于D,若CD=3,AB=8,则△ABD的面积12.
如图,Rt△ABC中,∠C=90°,BD是∠ABC的平分线,交AC于D,若CD=3,AB=8,则△ABD的面积12.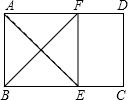 如图,在矩形ABCD中,∠A的平分线交BC于E,∠B的平分线交AD于F,求证:四边形ABEF是正方形.
如图,在矩形ABCD中,∠A的平分线交BC于E,∠B的平分线交AD于F,求证:四边形ABEF是正方形.